面试官:为啥 Redis 使用跳表 而不是使用 红黑树?
文章目录
大家好,这是大厂面试拆解–数据结构与算法系列的第2篇文章
如果你面试 或者工作中遇到相关问题,欢迎留言!
阅读本文 你获得如下收益
- ✅ 通过跳表了解,数组,哈希表,红黑树,B+ 数据结构不同使用场景。
- ✅ 从感觉理解 Map 容器 采用红黑树,Redis为采用跳表,Mysql采用B+ 存储 升级准确理解。
- ✅坚持思考,就会很酷!有错误的地方,请大家指正。这次采用对比 和可视化演示加速理解。
- 直接回答跳表有什么优点 不好回答?哈希表不支持范围查询,在坏情况下 查询性能退化o(n),跳表解决支持范围查询和 top k 查询。
- 直接回答跳表有什么优点 不好回答? 红黑树在输入有序数据,导致 不“平衡方式”,然后调整?跳表通过概率方式 保证与输入数据无关,插入链表后 不需要在调整 “平衡”
大纲如下:

用户故事
面试官:什么是跳表(Skip List)?
小义:我开始认真思考这个问题:
- 之前我研究得很透彻,但现在因为连续加班半年,已经忘得一干二净了,不知该如何回答。
- 紧张,自责,说出来你可能不信。
老王:打住,忘记很正常
- 过去半年想不明白的事情,就算再给你半年也想不明白
- 离开面试现场这个环境,回答到工作场景中去,同样因为加班这事情个优先级 高于学习这个事情,导致不停的推迟,无奈推迟,最后忘记。
- 可能感觉无用,可能是不知道从哪里下手 才是隐藏冰山下真正阻力,
- 就像一只公鸡投入长时间研究却仍然不会,会觉得丢人吗?同行会怎么看?其他鸡又会怎么看。 才是隐藏冰山下真正阻力
老王: 现在就是最好的时候,不是课下回家 在学习 。
- 现在你就是面试官,你刷题无数,这次你来面试别人一次,
- 现在你就是一个丰富经验的项目经理,你最清楚方案,这次你就来讨论这次方案
- 现在你就是领导,你根本不懂开发这个事情,这次你用权利让别人想你汇报。
画外音:
- 面试最忌讳的,需求是别人分析,代码是别人设计的,问题是别人解决–我干了啥
- 职场忌讳:什么有价值事情做什么,不是在不停加班1年做无用事情,别人不会多看你一眼睛, 职场不是慈善机构,判断事情标准发生变化。这也是什么整天开会,确定优先级,确定问题紧急程度。
- 想一想 哪怕不能100%去了解,但是看到了,听到,见到了,从第一行原理了解,私下吃饭 时候交流了?尝试上级争取了吗,不要受限于岗位,分工 ,这样不可控因素印象。
小义:
(1)假如我根本不懂 —>我就问
-
什么是跳表,
-
什么场景使用
-
什么场景不会使用
画外音:
- 我不了解,我等着你告我?让我相信。
- 太细节我听不懂,但是场景能使用,什么场景不能使用 我还是了解的。
(2) 假如我了解单链表,你了解到
- 单链表如何删除我清楚,必须查找到前面要一个元素。
- 单链表如何插入我清楚,至少定义2个指针。
—–> 我就会问 跳表插入,删除,查询步骤是什么?
(3)假如软件开发中经常使用 unordered_map,你了解到
- 数据结构是哈希表(hash table或者HashMap ,又称散列表,查询的平均时间复杂度 O(1)
- 哈希表 的key是唯一的,但是不同的key可能产生相同的hashCode,不同hashCode都落通一个bucket桶呢,在最坏情况下,查询时间时间复杂度复杂度 O(n)
- 在jdk1.8版本后,Java对HashMap做了改进,在链表长度大于8的时候,将后面的数据存在红黑树中,以加快检索速度
—–> 我就问:跳表是怎么查询的,时间 复杂度多少?
画外音:
- 链表查询一个元素时候,时间复杂度是o(n),不要发明新 算法,换个跳表这个结构可以吗?
- 能不活学活用 用跳表代替红黑树。
(4)假如你知道你在实时系统中经常使用map 存储业务数据。
- 经常用操作就是插入操作,删除操作 ,
- 并且 删除一个元素,其他迭代器(无论前向或后向)依然保持有效,不会受到影响。
- 红黑树天然更容易配合 STL 的语义(迭代器、顺序、稳定性)
- map 不支持并发,不考虑红黑树并发的问题。
—–> 我就问:什么情况下 redis为什么要使用skiplist跳表,不用 红黑树,hash表
画外音:
- 红黑树维护树的高度上没有AVL树,但是在插入和删除旋转较少更少,更适实时更新业务
- 不考虑并发问题
(5) 假如 我了解一点mysql数据库
-
查询:无法将数据全部加载进内存 ,需要将数据索引信息(主键),存储内存中,一般采用B+ 树索引
-
4 层的 B+ 存储220 亿条:
MySQL InnoDB 的实现,假设每个节点大小为 16KB,每个键为 8 字节,每个指针为 6 字节,则每个键指针对占用 14 字节。因此,每个非叶子节点最多可以包含约 1170 个键指针对。
在一个 4 层的 B+ 树中,结构如下:
- 第 1 层(根节点):1 个节点,包含约 1170 个指针,指向第 2 层的节点。
- 第 2 层:1170 个节点,每个节点包含约 1170 个指针,指向第 3 层的节点。
- 第 3 层:1170 × 1170 = 1,368,900 个节点,每个节点包含约 1170 个指针,指向第 4 层的叶子节点。
- 第 4 层(叶子节点):1170 × 1170 × 1170 ≈ 1.6 × 10^9 个节点。
如果每个叶子节点存储 16 条记录(假设每条记录为 1KB),则总共可以存储约:
1170 × 1170 × 1170 × 16 ≈ 2.2 × 10^10 条记录。(💡 这个地方没有累加,想象为什么)
因此,一个 4 层的 B+ 树在上述假设下,最多可以存储约 220 亿条记录
4 层的 B+ 存储220 亿条 占用256GB空间
- 第 1 层(根节点):
- 节点数:1
- 大小:1 × 4KB = 4KB
- 第 2 层:
- 节点数:400
- 大小:400 × 4KB = 1.6MB
- 第 3 层:
- 节点数:400 × 400 = 160,000
- 大小:160,000 × 4KB = 640MB
- 第 4 层(叶子节点):
- 节点数:400 × 400 × 400 = 64,000,000
- 大小:64,000,000 × 4KB = 256GB
4KB(第 1 层) + 1.6MB(第 2 层) + 640MB(第 3 层) + 256GB(第 4 层) ≈ 256.6GB
画外音:
- 4 层的 B+ 存储220 亿条 占用256GB空间 这些这些数据不需要全部加载内存
- 对于一个 4 层的 B+ 树,4KB(第 1 层) + 1.6MB(第 2 层) + 640MB ≈ 640MB 前三层的内部节点其实都可以存储在内存中,只有第四层的叶子节点才需要存储在磁盘中。
- 这样一来,我们就只需要读取一次磁盘即可。这也是为什么,B+ 树要将内部节点和叶子节点区分开的原因。
- 通过这种只让内部节点存储索引数据的设计,我们就能更容易地把内部节点全部加载到内存中了。
—–> 为什么MySQL用B+树而不用B树呢,跳表呢
—–> 如何使用B+树对海量磁盘数据建立索引
(6) 假如 我了解其他kv数据库,你可能了解到
- 如果是一个日志系统,每秒钟要写入上千条甚至上万条数据,这样的磁盘操作代价会使得系统性能急剧下降,甚至无法使用。
- B+ 树的数据都存储在叶子节点中,而叶子节点一般都存储在磁盘中。因此,每次插入的新数据都需要随机写入磁盘,而随机写入的性能非常慢。
—–> 为什么日志系统主要用LSM(Log Structured Merge Trees)树而非B+树?
划重点:
| 特性 | 🪜 跳表 (Skip List) | 🌳 红黑树 (Red-Black Tree) | 🧩 哈希表 (Hash Table) |
|---|---|---|---|
| 查找 - 平均 | O(logN) | O(logN) | O(1)(理想) |
| 查找 - 最坏 | O(logN) | O(logN) | ❌ O(n)(哈希冲突严重时) |
| 插入/删除 - 平均 | O(logN) | O(logN) | O(1) |
| 插入/删除 - 最坏 | O(logN) | O(logN) | ❌ O(n) |
| 是否有序 | ✅ 支持有序遍历 | ✅ 天生有序 | ❌ 无序 |
| 结构复杂度 | 中(链表+概率) | 高(旋转+颜色维护) | 中 |
| 实现难度 | 简单~中 | 高 | 中 |
| 空间开销 | 高(需多层索引) | 中 | 中(需哈希表+链) |
| 并发友好性 | ✅ 好(可分段加锁) | ❌ 差(全局旋转难并发) | 一般(需无锁/加锁) |
| 范围查找(如区间) | ✅ 支持 | ✅ 支持 | ❌ 不支持(只能找某个 key) |
| 典型使用场景 | Redis SortedSet | C++ STL map/set |
C++ unordered_map 等 |
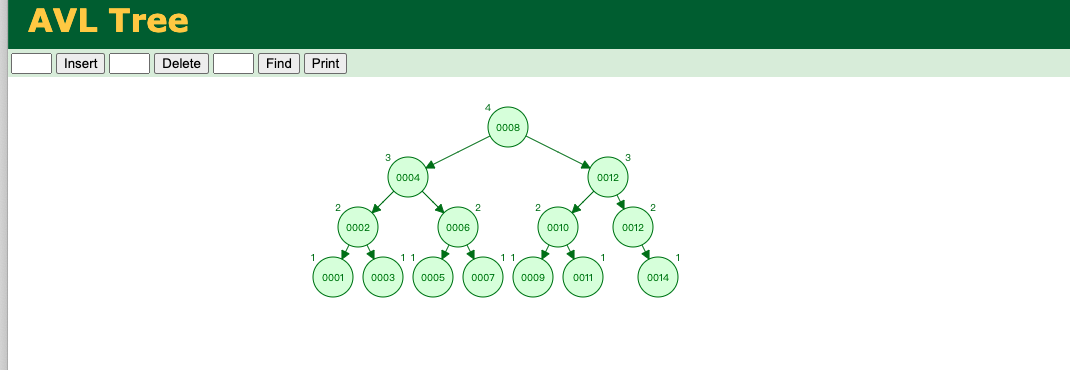
| 特性 | 🔵 AVL树 | 🔴 红黑树 |
|---|---|---|
| 查询效率 | ✅ 更快(更平衡) | 稍慢(不如AVL平衡) |
| 插入操作 | ❌ 慢一些,需要较多旋转(最多 O(logN) 次) | ✅ 快一些,旋转较少(最多 2 次) |
| 删除操作 | ❌ 最慢,重平衡代价高(最多 O(logN) 次旋转) | ✅ 快,最多 3 次旋转 + 染色 |
| 平衡条件 | 严格:任意节点左右子树高度差 ≤ 1 | 宽松:满足红黑规则即可 |
| 旋转次数 | 插入/删除时可能频繁,最多 O(logN) 次 | 插入最多 2 次,删除最多 3 次 |
| 使用场景 | 查询为主的场景,如数据库索引 | 插入/删除频繁,如 STL map/set、OS调度等 |
开始
问:什么是跳表,数据结构是什么(Redis实现为例子)
下面是我的理解:
定义:
- 支持范围查询**的 多层 有序链表
- 相比 单链表不支持随机查找,在插入一个元素 ,跳表在每个节点上随机产生多个指向下一个节点指针,指针个数层数
- 层数特点 (1) 跟输入数据顺序无关,这个根据概率生成器来产生的
- 层数特点 (2)在插入和删除之后 依然保持层数 平衡,不需要额外维护(其他平衡二叉在插入,删除一个之后破坏定义平衡关系需要调整)
| 维度 | 跳表 | 平衡树 |
|---|---|---|
| 实现复杂度 | 无需旋转/再平衡操作 | 需要复杂旋转和平衡维护逻辑 |
| 并发性能 | 天然支持高效并发操作 | 并发实现复杂 |
| 空间开销 | 平均1.33指针/元素 | 通常需要2-3指针/元素 |
| 查询性能稳定性 | 概率保证O(log n) | 严格保证O(log n) |
| 持久化结构 | 更易实现无锁版本 | 无锁实现难度大 |
数据结构:
|
|
小提示:
- 不可能像学物理,数学一样定义一个概念,一个共识,不需要这么严谨,根据特性拿出理解就行
- 直接放弃 课本上,网络上 对 跳表下定义
- 为了直观看看跳表构建的过程,可以使用 Claude3.5 做了一个跳表可视化页面。 可以指定跳表的最大层高,以及调整递增层高的概率, 然后可以随机初始化跳表,或者插入、删除、查找节点,观察跳表结构的变
- https://algo.hufeifei.cn/SkipList.html
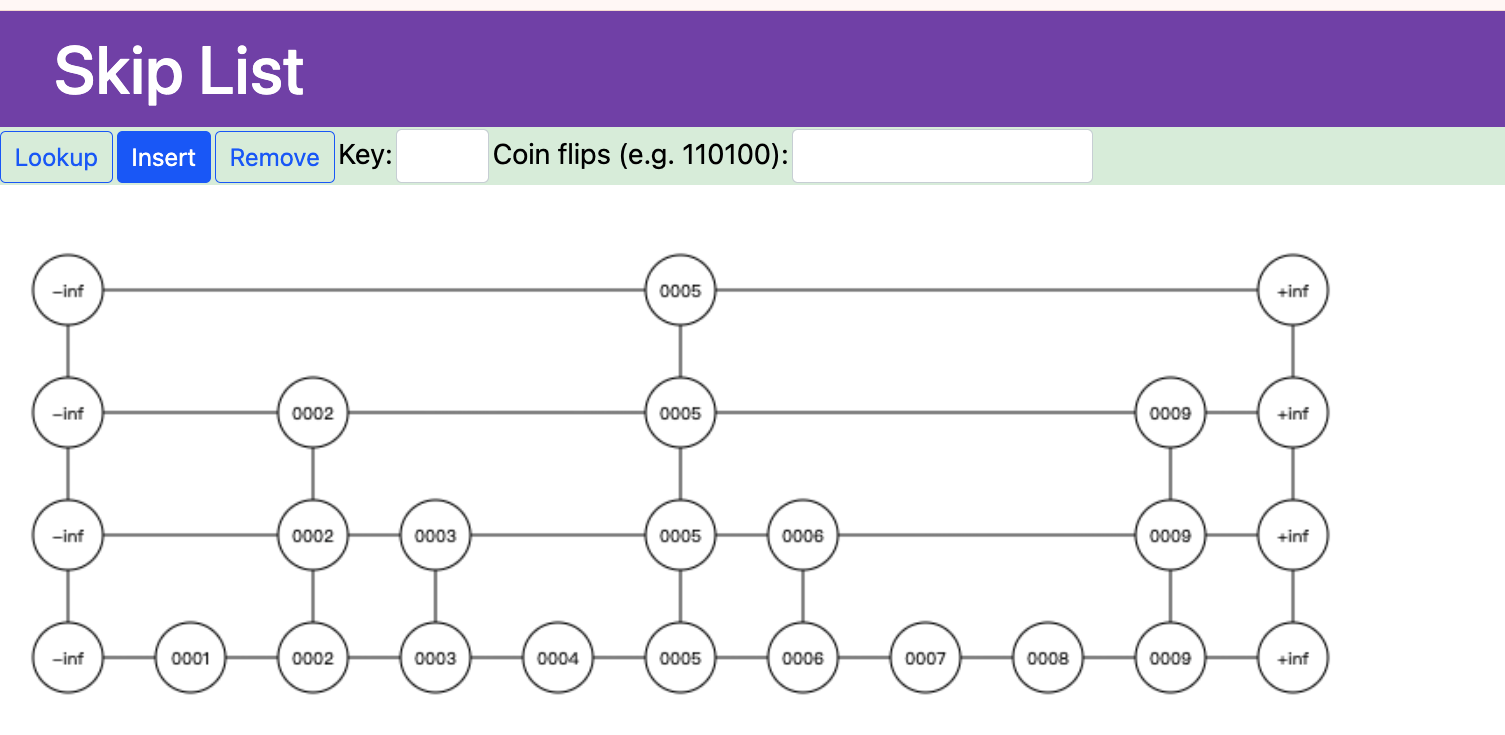
问:跳表 插入,删除,查找 基本步骤是什么
创建
|
|
插入操作:
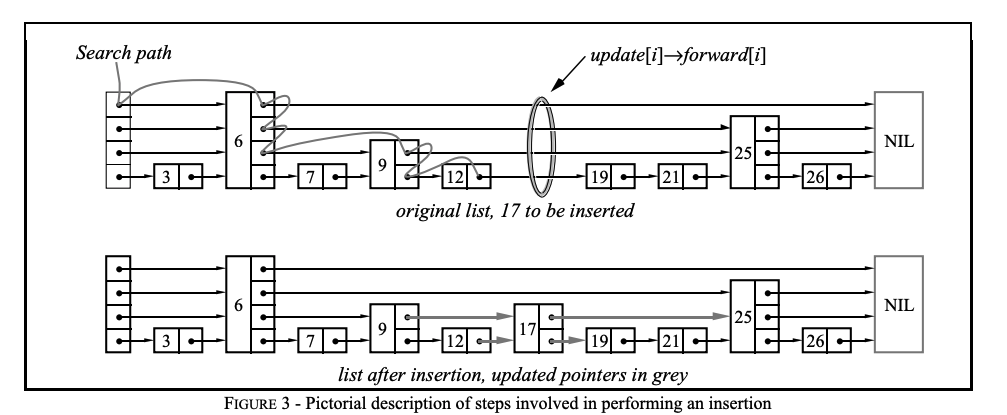
|
|
- 插入元素后 维护 前驱节点 和span。
- 控制高度
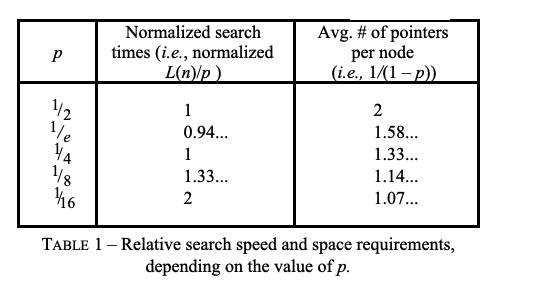
|
|
-
p=0.25(ZSKIPLIST_P),即:level=1概率:75%level=2概率:18.75%level=3概率:4.6875%- …
- 最大层级
ZSKIPLIST_MAXLEVEL=32
问:Map结构为什么采用红黑树
 红黑树为什么综合性能好?
红黑树为什么综合性能好?
-
在《算法(第4版)》中说过,红黑树等价于2-3树,换句话说,对于每个2-3树,都存在至少一个数据元素是同样次序的红黑树。
-
在2-3树上的插入和删除操作也等同于在红黑树中颜色翻转和旋转。这使得2-3树成为理解红黑树背后的逻辑的重要工具,这也是很多介绍算法的教科书在红黑树之前介绍2-3树的原因,尽管2-3树在实践中不经常使用。
其中2-节点等价于普通平衡二叉树的节点,3-节点本质上是非平衡性的缓存。
-
当需要再平衡(rebalance)时,增删操作时,2-节点与3-节点间的转化会吸收不平衡性,减少旋转次数,使再平衡尽快结束。
-
在综合条件下,增删操作相当时,数据的随机性强时,3-节点的非平衡性缓冲效果越明显。因此红黑树的综合性能更优。
继续追根溯源,红黑树的性能优势,本质上是用空间换时间。
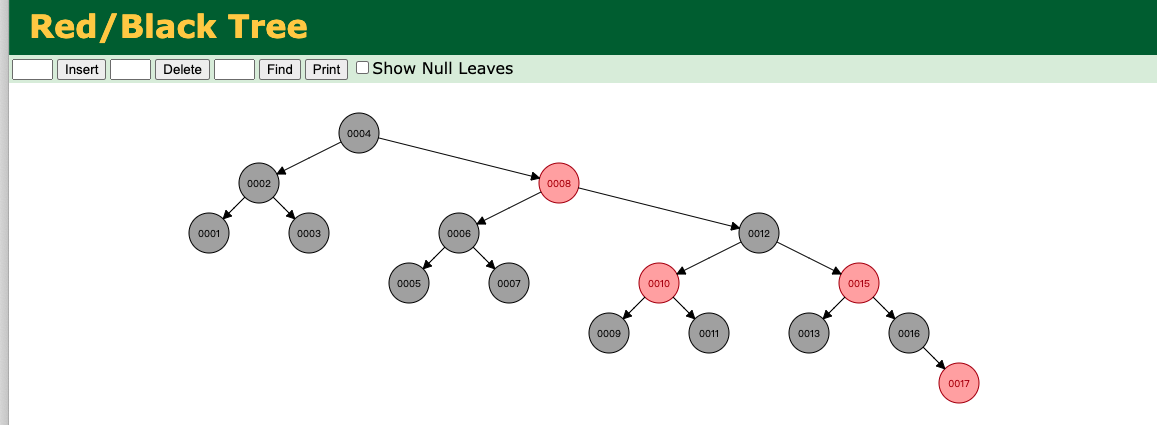
演示:https://algo.hufeifei.cn/RedBlack.html
问:Redis为什么用跳表skiplist,而不HashMap,红黑树?

- Redis 支持ZRANGE 范围查询,HashMap 是无序存储不支持范围查询,只能做单个key的查找,在最坏情况,哈希值冲突情况下,查找时间复增加到O(n)
- Redis 根据积分进行排行榜查询,也就是Top(k)问题,跳表支持。红黑树也指出,改造成本上跳表更低。红黑树要维护每个根节点上,增加
size字段,表示子树个数。 - Redis 采用单线程处理模型,因此不存在并发访问跳表的诉求。
- 如果未来 类似 rocksdb 则采用多线程处理模型,并发读写内存数据结构时,需要兼顾数据一致以及操作性能,此时就需要使用到并发安全的跳表结构.
- 跳过列表也非常适合并发多线程访问,尤其是更新和删除
- 如何控制平衡:输入有序插入时候,通过概率维护平衡 插入数据,而不是 先插入 破坏定义平衡 然后在调整容易的多(不能消除最坏 退化成单链表)。
Balancing a data structure probabilistically is easier than explicitly maintaining the balance 用概率来平衡数据结构比明确地维持平衡更容易
Skip lists are balanced by consulting a random number generator. Although skip lists have bad worst-case performance
随机数生成器来平衡
no input sequence consistently produces the worst-case performance (much like quicksort when the pivot element is chosen randomly).
Because these data structures are linked lists with extra pointers that skip over intermediate nodes, I named them skip lists 由于这些数据结构是带有额外指针的链表,这些指针可以跳过中间节点,因此我将它们命名为“跳过列表”
top k查询 对应原文:
Using skip lists, it is easy to do most (all?) the sorts of operations you might wish to do with a balanced tree such as use search fingers, merge skip lists and allow ranking operations (e.g., determine the kth element of a skip list)
划重点:
- 红黑树可以精准支持排名查询,理论上已有良好支持
- 强树就是 Order-Statistic Tree(顺序统计树),其底层就是红黑树,只是每个节点额外维护了
size字段。在插入、删除时维护size字段即可
|
|
- 为来更容易 理解 完成 count-complete-tree-nodes题目 统计节点个数
- 查询top k算法

画外音:
- 面试官:海量无序数据,寻找第 K 大的数,越快越好 就用skiplist好了。
问:数据库为采用B+ tree,放弃跳表/红黑树
- 4 层的 B+ 存储220 亿条 占用256GB空间, 前三层的内部节点其实都可以存储在内存中(640MB),只有第四层的叶子节点才需要存储在磁盘中(256GB)。—减少io访问次数
- B+树 可以利用索引的“最左前缀”来定位记录。—多个值进行排序
- 演示https://www.cs.usfca.edu/~galles/visualization/BPlusTree.html
问:数据库采用LSM 树,为什么放弃了B+ tree
- 这个后续专门写一篇文章。这里没有深入了解不过多讨论。
总结:(最坏情况分析)
- 数组支持随机访问,链表不支持随机访问
- 有序数组 采用二分查找 时间复杂度是O(logn),有序链表 查找一个元素时间复杂度o(n)。
- 哈希表支持key查询,不支持范围查询,最坏情况下,查询 hash冲突 性能下降o(n)
- 二叉搜索树 天然解决hash冲突问题,最坏情况 退化成单链表
- 红黑树 和avl都是平衡二叉查找树,在频繁插入和删除操作中,avl每个节点维护子树个数。红黑树最多2-3次 选装完成。【这个没有深入研究】
- 跳表 通过概率方式 维持平衡,根输入数据无关,在 插入和删除方面 不考虑插入后是否影影响平衡。
- 目前Redis 单线程操作跳表,但是跳表通过改造 非常适合并发多线程访问。(插入,删除后影响节点范围)
- 上面数据结构都是使用内存,不适合磁盘存储存储。
遗留任务
- https://leetcode.cn/problems/count-complete-tree-nodes/ 写算法统计节点个数
- 实现并发 无锁 跳表
- 跳表 不同语言 golang c++,java等实现。
- lsm tree
参考资料
- STL源码剖析 第三章 #迭代器与traits编程技法
- Redis 设计与实现
- Skip Lists: A Probabilistic Alternative to Balanced Trees
- http://zhangtielei.com/posts/blog-redis-skiplist.html
- https://news.ycombinator.com/item?id=1171423
- https://ketansingh.me/posts/lets-talk-skiplist/(go语言实现)
- order-statistic tree | augmented red-black tree | easy explained
- 数据结构算法可视化(MIT官方教材)
- https://gallery.selfboot.cn/zh/algorithms/skiplist
- 记一次生产慢sql查询的解决
- NoSQL检索:为什么日志系统主要用LSM树而非B+树?
- https://selfboot.cn/2024/09/09/leveldb_source_skiplist/
- https://visualgo.net/en ## 通过动画可视化数据结构和算法
链接我
如果对上面提到c++学习路径 推荐书籍感兴趣
关注公共号:后端开发成长指南 回复电子书
如果更进一步交流 添加 微信:wang_cyi

为什么写这篇文章
1. 目标:冲击大厂,拿百万年薪
- 想进入一线大厂,但在C++学习和应用上存在瓶颈,渴望跨越最后一道坎。
2. 现状:缺乏实战,渴望提升动手能力
-
公司的项目不会重构,没有重新设计的机会,导致难以深入理解需求。
-
想通过阅读优秀的源码,提高代码能力,从"不会写"到"敢写",提升C++编程自信。
-
需要掌握高效学习和实践的方法,弥补缺乏实战经验的短板。
3. 价值:成为优秀完成任务,成为团队、公司都认可的核心骨干。
优秀地完成任务= 高效能 + 高质量 + 可持续 + 可度量
错误示范:
- 不少同学工作很忙,天天加班,做了很多公司的事情。 但是 不是本团队事情,不是本部门事情,领导不认可,绩效不高
- 做低优先级的任务,无法利他,绩效不高
- 被招进来后可能随时被裁掉的一些征兆:
- 刻意提高工作难度
- 工作中遭受不公平对待
- 遭遇恶性竞争
- 被捧杀