开始日期	更新日期	备注
2020-6-10	2020-6-10	300-400中等难度总结

题目汇总

1. 查找和最小的K对数字
2. 合并K个排序链表
寻找两个有序数组的中位数
K个有序数组的中位数
m个有序数组求第k小的数字
有序矩阵中第K小的元素
[375] 猜数字大小 II
1. 搜索二维矩阵 II

373. 查找和最小的K对数字

一、题目信息

今天来做这个题目，主要考察的xxx

二、思路描述

能说出基本思想即可,实在不行动手画个流程图把。

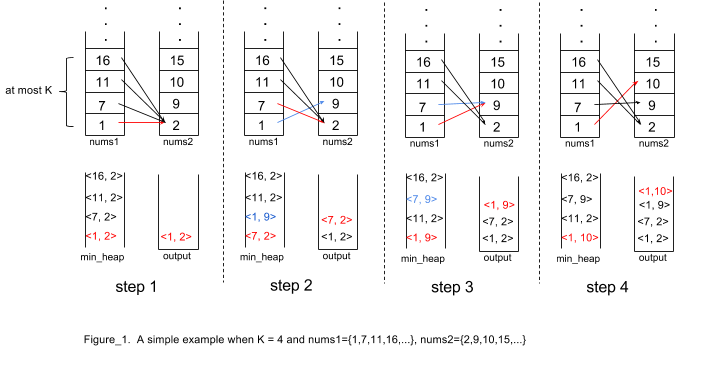
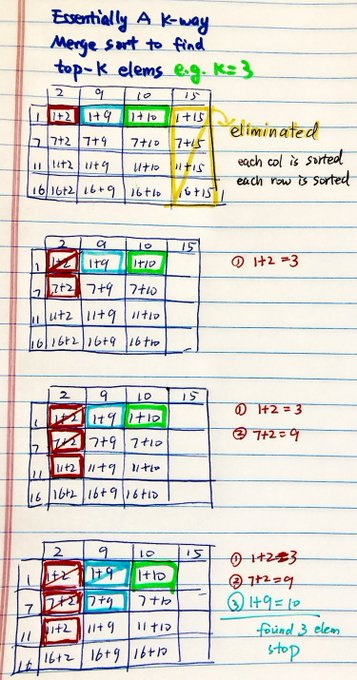
三、算法描述

算法是问题求解过程的一种描述,有清晰的操作步骤。

四、参考代码

放轻松，虽然是c++实现，我们一贯宗旨是拒绝奇技淫巧，不懂代码一看就明白

五、举一反三

别人最佳答案并不重要，关键是自己理解。 https://leetcode-cn.com/problems/find-k-pairs-with-smallest-sums/solution/cha-zhao-he-zui-xiao-de-kdui-shu-zi-by-lenn123/ https://leetcode.com/problems/find-k-pairs-with-smallest-sums/discuss/84551/simple-Java-O(KlogK)-solution-with-explanation

[375] 猜数字大小 II

一、题目信息

今天来做这个题目，主要考察的xxx

链接：guess-number-higher-or-lower-ii

来源：Interview Question

难度：中等

二、题目描述

算法是问题求解过程的一种描述，看看这个题目是怎么描述的吧。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22


 * 我们正在玩一个猜数游戏，游戏规则如下：
 * 
 * 我从 1 到 n 之间选择一个数字，你来猜我选了哪个数字。
 * 
 * 每次你猜错了，我都会告诉你，我选的数字比你的大了或者小了。
 * 
 * 然而，当你猜了数字 x 并且猜错了的时候，你需要支付金额为 x 的现金。直到你猜到我选的数字，你才算赢得了这个游戏。
 * 
 * 示例:
 * 
 * n = 10的, 我选择了8.
 * 
 * 第一轮: 你猜我选择的数字是5，我会告诉你，我的数字更大一些，然后你需要支付5块。
 * 第二轮: 你猜是7，我告诉你，我的数字更大一些，你支付7块。
 * 第三轮: 你猜是9，我告诉你，我数字更小一些，你支付9块。
 * 
 * 游戏结束。8 就是我选的数字。
 * 
 * 你最终要支付 5 + 7 + 9 = 21 块钱。
 * 
 * 
 * 给定 n ≥ 1，计算你至少需要拥有多少现金才能确保你能赢得这个游戏。

三、算法描述

能说出基本思想即可,实在不行动手画个流程图把。

Solution1 题目看起来很简单，但是无从下手。 n是模糊数据。最差就是（1+n）n/2 顺猜，优化一下平衡二叉搜索tree，但是结果如何计算呢？

画外音：在此阅读题目要求，自己理解题目了吗？对不明白地方，我跳过了吗?

给定 n ≥ 1，计算你至少需要拥有多少现金才能确保你能赢得这个游戏 <—> 需要考虑最坏情况下的代价。也就是说要算每次都猜错的情况下的总体最大开销。

四、参考代码

放轻松，虽然是c++实现，我们一贯宗旨是拒绝奇技淫巧，不懂代码一看就明白

五、举一反三

别人最佳答案并不重要，关键是自己理解。 https://zxi.mytechroad.com/blog/dynamic-programming/leetcode-375-guess-number-higher-or-lower-ii/

[377] 组合总和 Ⅳ

一、题目信息

这个是一个经典题目,

第一次实现用递归回溯，参考组合排序,区别不需要判断历史记录是否访问，虽然做了剪彩。结果超时、
第二次实现，根据当target=1000时候，很多重复，采用vectordp(target+1,-1)) ,map<int,int>dp 虽然dp节省空间，但是依然耗时增加了
第三次实现，动态规划。和递归相比，递归是中间结果防止过度计算。动态规划是vectordp(target+1,0))，每个节点从小到大计算一次。变化公式target-array[i]
总结，动态规划是每个target都要计算一次。每个target如何计算和回溯一样，target-array[i]。这样一比较时间复杂度是降低的，但是递归浪费更多空间。

二、题目描述

算法是问题求解过程的一种描述，看看这个题目是怎么描述的吧。

给出一个都是正整数的数组 nums，其中没有重复的数。从中找出所有的和为 target 的组合个数～～～ nums = [1, 2, 3] target = 4

所有可能的组合为： (1, 1, 1, 1) (1, 1, 2) (1, 2, 1) (1, 3) (2, 1, 1) (2, 2) (3, 1)

来源：力扣（LeetCode）链接：https://leetcode-cn.com/problems/combination-sum-iv 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。～～～

三、算法描述

能说出基本思想即可,实在不行动手画个流程图把。

Solution1 递归回溯–当n过大时超时

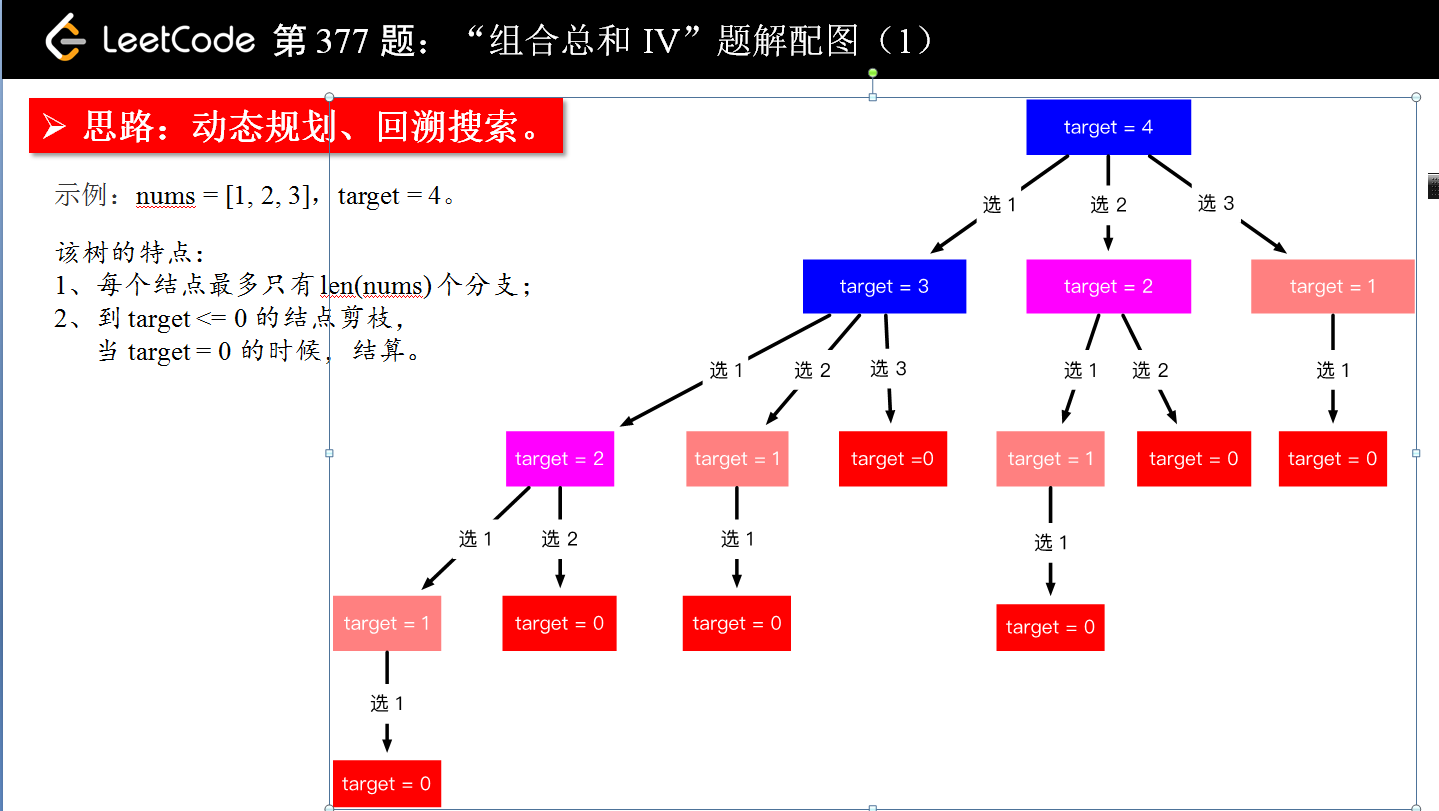
循环条件是：target 大于0

Solution2 从小到大的动态规划循环条件是：遍历target。

I=1

1+2 1+3 1+1

四、参考代码

放轻松，虽然是c++实现，我们一贯宗旨是拒绝奇技淫巧，不懂代码一看就明白

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67



class Solution
{
public:
    int combinationSum4(vector<int> &nums, int target)
    {
        vector<unsigned int> dp(target + 1, 0); //默认为0
        dp[0] = 1;                              // target=4 集合{4} 4-4=0;

        //动态规划，从小到大每个Indextarget都要计算,全部要计算。
        for (int targetIndex = 1; targetIndex <= target; targetIndex++)
        {
            //分叉
            for (int j = 0; j < nums.size(); j++)
            {
                //和为给定目标正整数的组合
                if (targetIndex >= nums[j])
                {
                    dp[targetIndex] += dp[targetIndex - nums[j]];
                }
            }
        }

        return dp[target];
    }
};


//@lc code=start
// 用map代替vector 虽然节省空间，但是时间增加了
// 40 ms  8.2 MB
class Solution4
{
private:
    unordered_map<int, int> map;

public:
    //驱动点
    int combinationSum4(vector<int> &nums, int target)
    {
        if (target < 0 || nums.empty())
            return 0;

        if (target == 0)
        {
            return 1;
        }

        if (map.count(target))
        {
            return map[target];
        }
        int count = 0;
        for (int i = 0; i < nums.size(); i++)
        {
            if (target >= nums[i])
            {
                cout << "-------------" << count << endl;
                count += combinationSum4(nums, target - nums[i]);
            }
        }

        map[target] = count;
        cout << target << ":" << count << endl;
        return count;
    }
};

五、举一反三

别人最佳答案并不重要，关键是自己理解。

378. 有序矩阵中第K小的元素

一、题目信息

今天来做这个题目，主要有3个思路，二分查找，虽然巧妙，但是理解不了，我没有做出来。

二、题目描述

算法是问题求解过程的一种描述，看看这个题目是怎么描述的吧。

二、题目描述

算法是问题求解过程的一种描述，看看这个题目是怎么描述的吧。

三、算法描述

能说出基本思想即可,实在不行动手画个流程图把。

空间 O(n)，时间Klg(n)

由于优先队列使用堆实现，可保证队列头是最小值

设矩阵有n行，这队列中有n个元素，每个元素都来自其中一行。初始化时，将每行的第0列压入

每次取出一个元素，根据元素是哪一行的，再将其所在行的下一个元素加入

执行k次出队列操作，即可得到结果

队列中每个元素为pair<int,pair<int,int»，外层pair的int表示矩阵中的值，内层pair的first表示第几行，内层pair的second表示该行的第几列

四、参考代码

放轻松，虽然是c++实现，我们一贯宗旨是拒绝奇技淫巧，不懂代码一看就明白

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140


//168 ms
class Solution
{
public:
    //仿函数
    struct compare
    {
        bool operator()(pair<int, pair<int, int>> &p1, pair<int, pair<int, int>> &p2)
        {
            // “大于” 构造的是最小堆
            return p1.first > p2.first;
        }
    };
    int kthSmallest(vector<vector<int>> &matrix, int k)
    {
        priority_queue<pair<int, pair<int, int>>, vector<pair<int, pair<int, int>>>, compare> pq;
        int cols, rows;
        rows = matrix.size();
        cols = matrix[0].size();
        //将每一行的第0列入队
        for (int i = 0; i < rows; ++i)
            pq.push(make_pair(matrix[i][0], make_pair(i, 0)));

        int res = 0;
        while (k)
        {
            res = pq.top().first;
            //记录堆顶元素所在的行、列
            int r = pq.top().second.first;
            int c = pq.top().second.second;
            pq.pop();
            --k;
            if (c + 1 < cols)
                pq.push(make_pair(matrix[r][c + 1], make_pair(r, c + 1)));
        }
        return res;
    }
};

class Solution2
{
public:
    int kthSmallest(vector<vector<int>> &matrix, int k)
    {
        auto comp = [&matrix](pair<int, int> p1, pair<int, int> p2) {
            return matrix[p1.first][p1.second] > matrix[p2.first][p2.second];
        };
        priority_queue<pair<int, int>, vector<pair<int, int>>, decltype(comp)> que(comp);
        que.push(make_pair(0, 0));
        int count = 1;
        while (count < k)
        {
            auto temp = que.top();
            que.pop();
            cout << "temp.first= " << temp.first << " temp.second " << temp.second << " value= " << matrix[temp.first][temp.second] << endl;
            if (temp.first + 1 < matrix.size())
            {
                que.push(make_pair(temp.first + 1, temp.second));
            }
            //if (temp.first == 0 && temp.second + 1 < matrix[0].size())
            if (temp.first == 0 && temp.second + 1 < matrix[0].size())
            {
                que.push(make_pair(temp.first, temp.second + 1));
            }
            count++;
        }
        auto t = que.top();
        return matrix[t.first][t.second];
    }

    /***  次方法虽然秒，但是我看不懂，并且体会里面好出，为什么大家都这样做。
      *  利用题目给出条件：有序  采用二分查找。
      *  
      *  二分查找关键 最大值，最小值,和中间值（卡住了）
      *  求top k  k是索引。array{k} ==中间值
      *  
      * 时间复杂度其实也是很高的
      * 1.找出二维矩阵中最小的数left，最大的数right，那么第k小的数必定在left~right之间
        2.mid=(left+right) / 2；在二维矩阵中寻找小于等于mid的元素个数count
        3.若这个count小于k，表明第k小的数在右半部分且不包含mid，即left=mid+1, right=right，又保证了第k小的数在left~right之间
        4.若这个count大于k，表明第k小的数在左半部分且可能包含mid，即left=left, right=mid，又保证了第k小的数在left~right之间
        5.因为每次循环中都保证了第k小的数在left~right之间，当left==right时，第k小的数即被找出，等于right 
          (76 ms ）
      */
    int kthSmallest1(vector<vector<int>> &matrix, int k)
    {
        int rows = matrix.size();
        if (0 == rows)
            return -1; //不存在
        int cols = matrix[0].size();
        //1 5 9 10 11 11 12 13 13 15
        // k=8 13
        // matrix = [
        //     *⁠[1, 5, 9],
        //     *⁠[10, 11, 13],
        //     *⁠[12, 13, 15] *
        // ],
        int low = matrix[0][0];
        int high = matrix[rows - 1][cols - 1];

        int mid = 0; //中间数值，array中是不存在的，通过计算是否第k小，变化low 和high的范围。

        while (low < high)
        {
            cout << low << "aaa" << mid << " " << high << endl;
            mid = low + (high - low) / 2;
            int count = findNotBiggerThanMid(matrix, mid);
            if (k > count)
            {
                low = mid + 1; //此时 low 变成可能不存。
            }
            else
            {
                high = mid;
            }
            cout << low << "bbb" << mid << " " << high << endl;
        }

        return low;
    }
    //查找一个元素
    int findNotBiggerThanMid(vector<vector<int>> &matrix, int x)
    {
        int N = matrix.size();
        int i = N - 1, j = 0, count = 0;
        while (i >= 0 && j < N)
        {
            if (matrix[i][j] <= x)
            {
                count += (i + 1);
                //排除列
                j++;
            }
            else
                //排除行
                i--;
        }
        return count;
    }
};

五、举一反三

别人最佳答案并不重要，关键是自己理解。

其他参考

https://leetcode-cn.com/problems/kth-smallest-element-in-a-sorted-matrix/solution/er-fen-fa-by-powcai-5/

leetcode_medium_300-400

文章目录

题目汇总

373. 查找和最小的K对数字

一、题目信息

二、思路描述

三、算法描述

四、参考代码

五、举一反三

[375] 猜数字大小 II

一、题目信息

二、题目描述

三、算法描述

四、参考代码

五、举一反三

[377] 组合总和 Ⅳ

一、题目信息

二、题目描述

三、算法描述

四、参考代码

五、举一反三

378. 有序矩阵中第K小的元素

一、题目信息

二、题目描述

二、题目描述

三、算法描述

四、参考代码

五、举一反三

其他参考