这是 «算法之美»系列第四篇 文章

  • 题目：数组中的第K个最大元素

  • 主要考察的 时间复杂度如何推算出来

    1. 提示1. 思路2 采用快速选择排序：为什么平均时间复杂度: O(n)，而不是O(nlog⁡n) ，最坏情况优化方式 vs 严蔚敏《数据结构》标准分割函数区别？
    2. 提示2: 堆排序 建队时间为什么: O(n) image.png

  • 难度：中等

  • 分类：数组,排序

一、为什么刷题

小王同学在拿到一个题目时候 ，总是不自觉遇到如下问题

❌ 阿里，腾讯 字节 三面算法太难了，根本无法通过，刷题还有什么意义，摆摆浪费时间。 ✅ 在学习算法过程中，放弃各种复杂技巧，学习不是为了读者感觉高大名词引入复杂设计。

❌这么多题目 你刷的过来吗，整天加班没时间。 ✅ 专注数据接结部分，这个可能来源项目，例如数据库，存储，操作系统，并不一定通过题目全完成获取。

❌ 周围人都不做，厉害人根不做，我做什么？ ✅ 不要指望别人，公司安排组织一起学习，这自己kpi。

二、 如何刷题

  • 解决这个问题，采用数据数据结构（对应上学课本大纲）
  • 数据结构基本操作优缺点是什么？（与项目中使用 增删改查方法结合起来）
  • 采用什么算法完实现什么功能（对应比赛，算法课程大纲）

image.png

三. 数组中的第K个最大元素

215. Kth Largest Element in an Array

Given an integer array nums and an integer k, return the kth largest element in the array.

Example 1: Input: nums = [3,2,1,5,6,4], k = 2 Output: 5

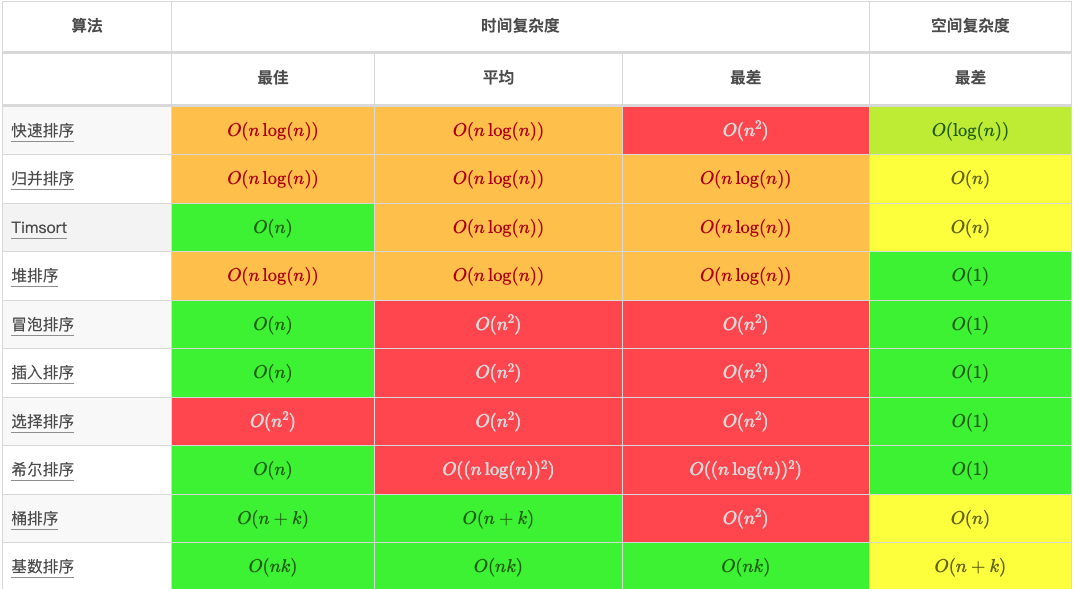
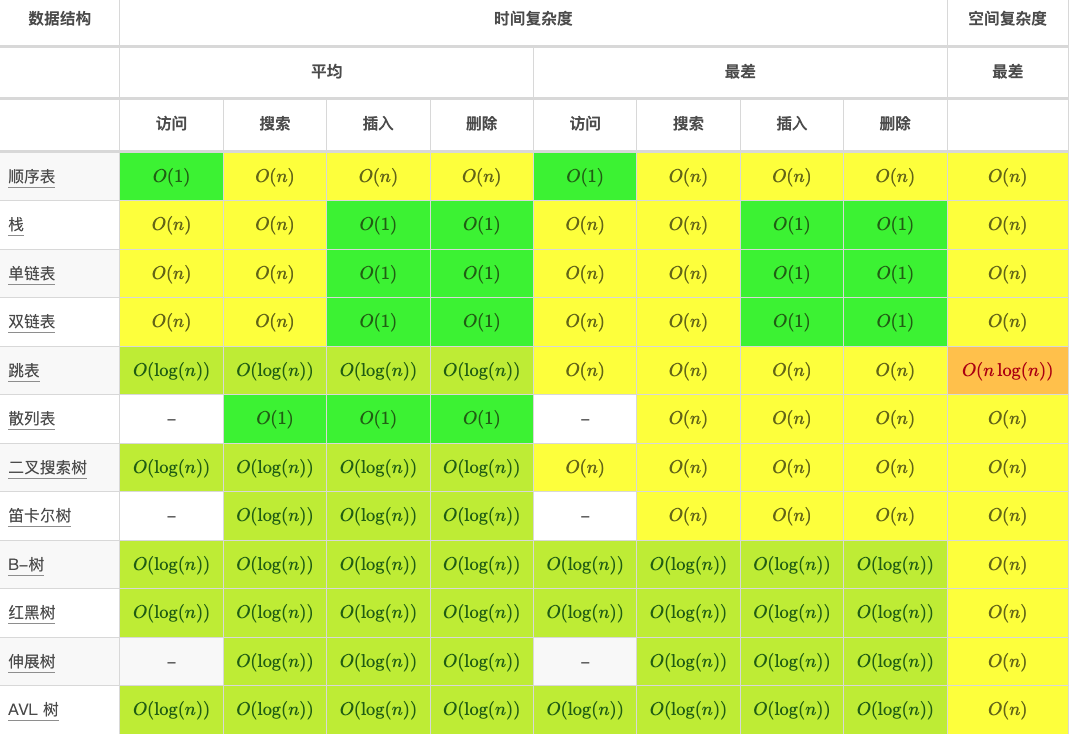
思路1:数组全部排序，然后选择 第k大元素

排序时间复杂度

常见数据结构

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) {
        // 获取数组的大小
        int size = nums.size();
        
        // 对数组进行升序排序
        sort(begin(nums), end(nums));
        
        // 返回第 k 大的元素（从后往前数第 k 个元素）
        return nums[size - k];
    }
};

时间复杂度 能在优化吗？

思路2:基于快速排序

image.png

我们要找到第 k 个最大元素 number，实际上我们并不关心比它大和比它小的那些元素的具体排序。

我们只希望那些比 number大的元素都集中到其左侧，比它小的元素都集中到其右侧，那么 nums[k-1] 就是第 k 个最大元素。【排序了又没完全排】

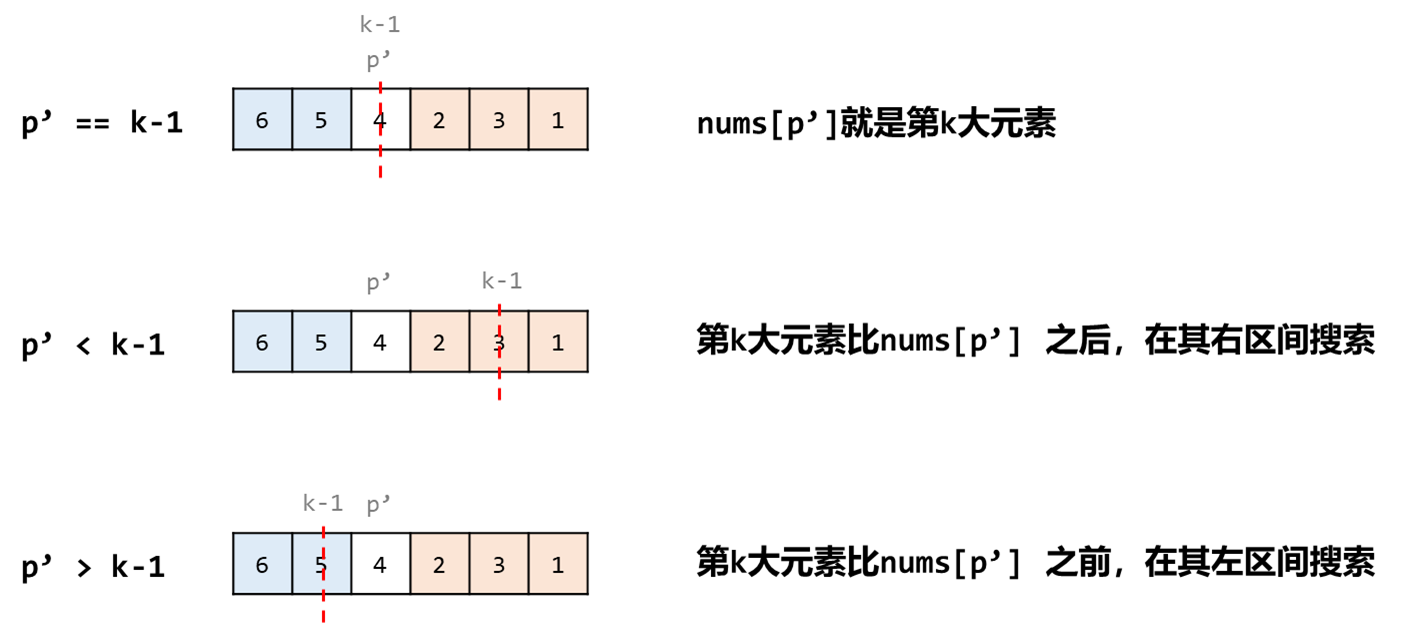
如果 不是怎么办？ image.png

如上图所示，这么一次操作后就可以确定选择的元素 nums[p] 的顺序了。假设其当前位置为 p'，则有以下三种情况：

  • p' == k-1，找到了第 k 大的元素，直接返回；
  • p' < k - 1，说明第 k 大的元素是比当前元素 nums[p]要靠后的，在其右侧区间进行递归搜索。
  • p' > k - 1，说明第 k 大的元素是比当前元素 nums[p]要靠前的，在其左侧区间进行递归搜索
小王疑问：平均时间复杂度: O(n)，而不是O(nlog⁡n)，这个是怎么计算的？遇到最坏情况怎么处理？

  • 在平均情况下，每次划分都比较平衡

  • 第一次划分需要处理 n 个元素

  • 第二次划分需要处理 n/2 个元素

  • 第三次划分需要处理 n/4 个元素

  • 以此类推…

  • 总和可以表示为：无穷等比数列 n + n/2 + n/4 + n/8 + … = 2n

补充：时间复杂度 image.png

最坏时间复杂度: O(n²)

  • 当数组已经排序或者所有元素都相同时会出现

  • 每次划分都极度不平衡（比如每次都把数组划分成 1 和 n-1 个元素）

  • 需要递归 n 次，每次需要遍历 n 个元素

最坏时间复杂度

c++代码（看不懂对着手敲一边，一定要动手）

特性 内容
分区方式 左右指针对撞法（Hoare）
兼容性 更符合你原来的代码风格
防止超时 引入随机 pivot
快速选择 保持 O(n) 平均复杂度 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) {
        int n = nums.size();
        return quickSelect(nums, 0, n - 1, n - k); // 第k大的数 == 第(n-k)小
    }

    int quickSelect(vector<int>& nums, int left, int right, int k_smallest) {
        if (left >= right) return nums[left]; //结束条件，返回值 ？？

        // 随机选择 pivot 避免退化
        int pivot_index = left + rand() % (right - left + 1);
        int pivot_final = partition(nums, left, right, pivot_index);

        if (pivot_final == k_smallest) {
            return nums[pivot_final];
        } else if (pivot_final > k_smallest) {
            return quickSelect(nums, left, pivot_final - 1, k_smallest);
        } else {
            return quickSelect(nums, pivot_final + 1, right, k_smallest);
        }
    }

    // 不使用 swap，采用左右移动方式分区
    //对比和严蔚敏《数据结构》标准分割函数区别是什么？
    int partition(vector<int>& nums, int left, int right, int pivot_index) {
        int pivot = nums[pivot_index]; // ----中间值 ，不一定 在最left 
        nums[pivot_index] = nums[left]; // 将 pivot 移到最左边，保存其值，为什么
        int i = left;
        int j = right;

        while (i < j) {
            while (i < j && nums[j] >= pivot) j--; // 从右向左找小于 pivot 的
            nums[i] = nums[j];                     // 右侧元素填到左边空位

            while (i < j && nums[i] <= pivot) i++; // 从左向右找大于 pivot 的
            nums[j] = nums[i];                     // 左侧元素填到右边空位
        }

        nums[i] = pivot; // 最后将 pivot 填入正确位置
        return i;        // 返回 pivot 的最终位置
    }
};
  • 对比差别 对left 预留位置
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

//严蔚敏《数据结构》标准分割函数
 int Paritition1(int A[], int low, int high) {
   int pivot = A[low];
   while (low < high) {
     while (low < high && A[high] >= pivot) {
       --high;
     }
     A[low] = A[high];
     while (low < high && A[low] <= pivot) {
       ++low;
     }
     A[high] = A[low];
   }
   A[low] = pivot;
   return low;
 }

 void QuickSort(int A[], int low, int high) //快排母函数
 {
   if (low < high) {
     int pivot = Paritition1(A, low, high);
     QuickSort(A, low, pivot - 1);   //全部排序
     QuickSort(A, pivot + 1, high); // 
   }
 }

思路3:堆排序

假设 建立一个 最小堆（小顶堆）大小为 k最小堆，始终保存当前遇到的 最大的 k 个元素。

  • 此时堆顶是这 k 个元素中 最小的那个，等于m
  • 如果新插入一个元素n，如果当前元素 比 堆顶最小值还小。n < m, 一定不是跳过
  • n 大于 m，说明 m一定不是，当前的m
  • 所以，当遍历完所有元素后，堆顶就是 第 k 大的元素。
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29


//总时间复杂度为 O(n log k)

// 空间复杂度：O(k) - 需要维护一个大小为 k 的堆

class Solution {

public:

int findKthLargest(vector<int>& nums, int k) {

	priority_queue<int, vector<int>, greater<int>> pq;
	
	for (auto n : nums) 
	{   
	    //n 不可能是第第k大的元素 这个优化点
		if (pq.size() == k && pq.top() >= n) continue;
		
		if (pq.size() == k) {
			pq.pop();
		}
	    pq.push(n);
  }.   
  
  return pq.top();
}

};

📌 举个例子：

我们要找第 k = 3 大的数，当前堆是：

pq = [5, 6, 7，] // 注意是最小堆，堆顶是 5

现在来个新数 n = 3：

  • pq.size() == 3

  • pq.top() = 5，而 n = 3 更小

➡️ 那么 3 比当前 k 大的最小数还小，肯定排不进前 3 大，直接跳过！

参考