成为孩子榜样,为国争光
文章目录

知识地图:从信奥赛 CSP-J/S到Leetcode 拓扑排序-课程表 题目难度:这个是高中省级比赛 ,题目有点难,小学组不要对号入座,
各位老师好 ,我是小义, 今天是6月4
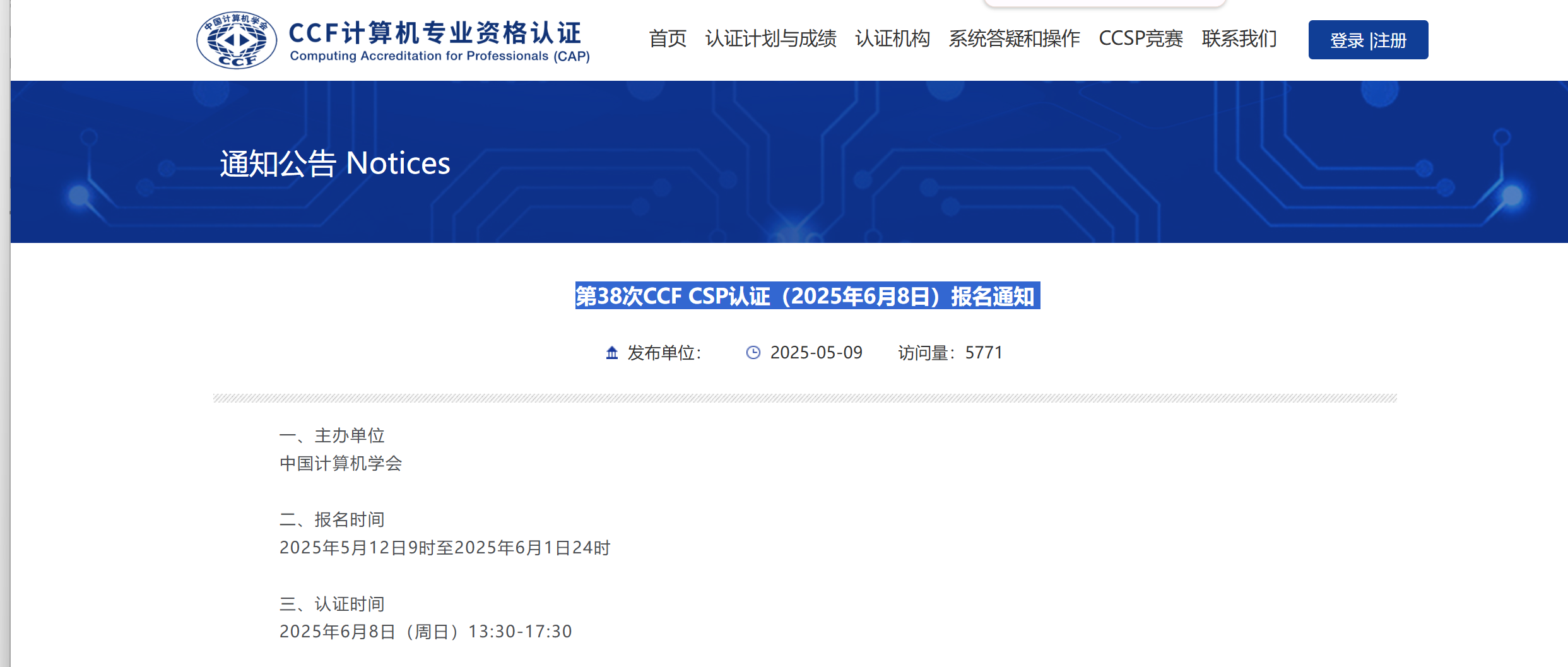
- 距离2025年9月16日第38次CCF计算机软件能力考试CSP-J/S 还有104天
- CSP-J/S 考试报名:2025年5月12日–2025年6月1日
- 孩子们,无论报名成功的还是没有报名成功的,从现在准备的充分 去CSP-J/S战场上检验自己的学习成果。
- 距离2025年毕业季还有24天 (不同学校不同都在6月或者7月中旬左右)
- 实习找工作师弟师妹 抓紧了, Leetcode刷题必不可少。
- 小学初中:参加信奥比赛想要CSP-J/S 想要历年真题
- 校招:找工作实习想要内推码
- 社招:大厂内推 联系我 ,围绕数据结构与算法 这个事情一起努力
本文大纲: 第一步:建立大局观 刷题有什么用 第二步:构建知识地图: 针对知识点有效训练 第三步:专心刷1题:课程表
第一步:把枯燥刷题变成伟大事情(有啥用 阅读耗时2分钟)
 信息学奥赛,简称为“信奥”,说来话长;
1984年邓小平同志提出:“计算机的普及要从娃娃做起。”
于是,中国计算机学会在当年就创办了全国青少年计算机程序设计竞赛,
本质上就是,面向中学生的计算机编程大赛
信息学奥赛,简称为“信奥”,说来话长;
1984年邓小平同志提出:“计算机的普及要从娃娃做起。”
于是,中国计算机学会在当年就创办了全国青少年计算机程序设计竞赛,
本质上就是,面向中学生的计算机编程大赛
竞赛旨 在向那些在中学阶段学习的青少年普及计算机科学知识 给那些有才华的学生提供相互交流和学习的机会;
使用场景与目标人群
- NOI:主要服务于中学生竞赛升学
- LeetCode:面向求职者(尤其是软件工程师)及编程爱好者,用于提升面试通过率或日常技能训练。
2.1 辅导自己小孩,邻居小孩,社区小孩 参加CSP-J比赛
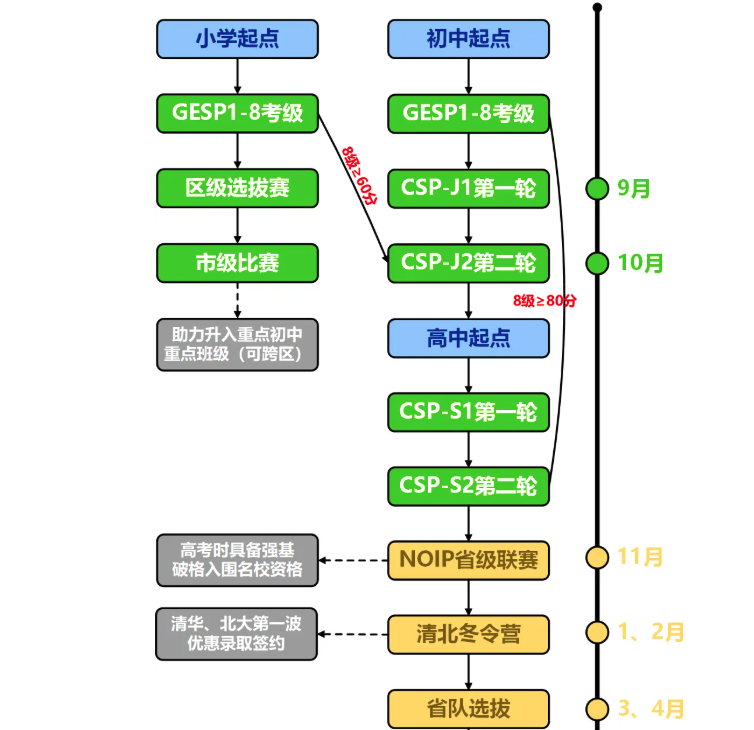
CSP、NOIP、NOI这三个比赛都是由中国计算机学会(CCF)举办的, 代表同学们在编程竞赛上的不同阶段: 1. CSP-J(入门级,Junior) :主要针对小学和初中生 2. CSP-S(提高级,Senior):CSP-S面向高中生 3. NOIP:省选,NOIP名额有限,NOIP是参加NOI的必要条件 4. NOI:国赛,为国争光
从CSP-J/S到NOI,信竞之路一路走来实属不易。 希望走信息学路线的孩子都能抓住每一次比赛机会,夺得奖项。 纵使有成绩不如意的时候,也要戒骄戒躁,不要轻言放弃。
2.3 等级划分
CSP 入门级
CSP 入门级(CSP-J),前身是 NOIP 普及组,是 NOI 系列赛事中难度最低,面向年龄最低的赛事,它是很多学生参与的第一个信息学的大型比赛。
- 适宜年龄:11-14 岁。
- 比赛时间:第一轮为 9 月,第二轮为 10 月。
- 比赛形式:第一轮为 2 小时的笔试,第二轮为 3.5 小时的上机测试。全国统一命题,省级评奖。
- 竞赛优惠:对小升初、初升高皆有帮助(取决于地方性政策)。部分知名初高中会对在 CSP-J 比赛中取得优秀成绩的选手(一般来说是一等)提供录取或者分班优惠政策。
- 参考训练量:于“洛谷”上完成 80 个“普及”难度的试题。历届试题可在“洛谷”上搜索。
CSP 提高级
CSP 提高级(CSP-S)主要面向广大的初高中生,难度较入门级有着显著提升,其含金量也显著更高。CSP-S 的成绩是学生参与后续的 NOI 系列赛事的重要凭证。
- 适宜年龄:12-17 岁。
- 比赛时间:与 CSP 入门级相同,第一轮为 9 月,第二轮为 10 月。
- 比赛形式:第一轮为 2 小时的笔试,第二轮为 4 小时的上机测试。全国统一命题,省级评奖。
- 竞赛优惠:对初升高有很大帮助。在 CSP-S 中取得优秀成绩(一般也是一等)的学生多会被顶级高中(如北京人大附中、上海华师大二附中、浙江杭州二中)等特招。
- 参考训练量:于“洛谷”上完成 150 个“提高”难度的试题,50 个“提高+”难度的试题。历届试题可在“洛谷”上搜索。
NOIP
全国青少年信息学奥林匹克联赛(NOIP)面向高中生群体,难度较 CSP-S 有一定提升,是绝大多数参与信息学竞赛的选手能够接触到的含金量最高的赛事。
-
适宜年龄:15-17 岁。
-
比赛时间:11 月中下旬。
-
比赛形式:4.5 小时的上机测试。全国统一命题,省级评奖。
-
竞赛优惠:NOIP 中获得一等奖将会在知名大学的少创班、综合评价测试、专项初审环节中取得显著优势。
-
参考训练量:于“洛谷”上完成 200 个“提高”难度的试题,100 个“提高+”难度的试题。历届试题可在“洛谷”上搜索。
完整地址:https://docs.qq.com/sheet/DY1NwcGZjUXpYb01j?tab=oqi27u
2.2 刷题Leetcode找工作,进大厂,去外企
- 面试大厂必要条件,太卷了
- 去亚马逊,微软等外企必要条件
- 一定要刷题吗?不一定,创业公司 更看重项目经验
- 无论什么公司,数据结构与算法都是基本功
- 必须完成300题目
第二步:构建知识地图( 怎么做,约定耗时 2分钟)
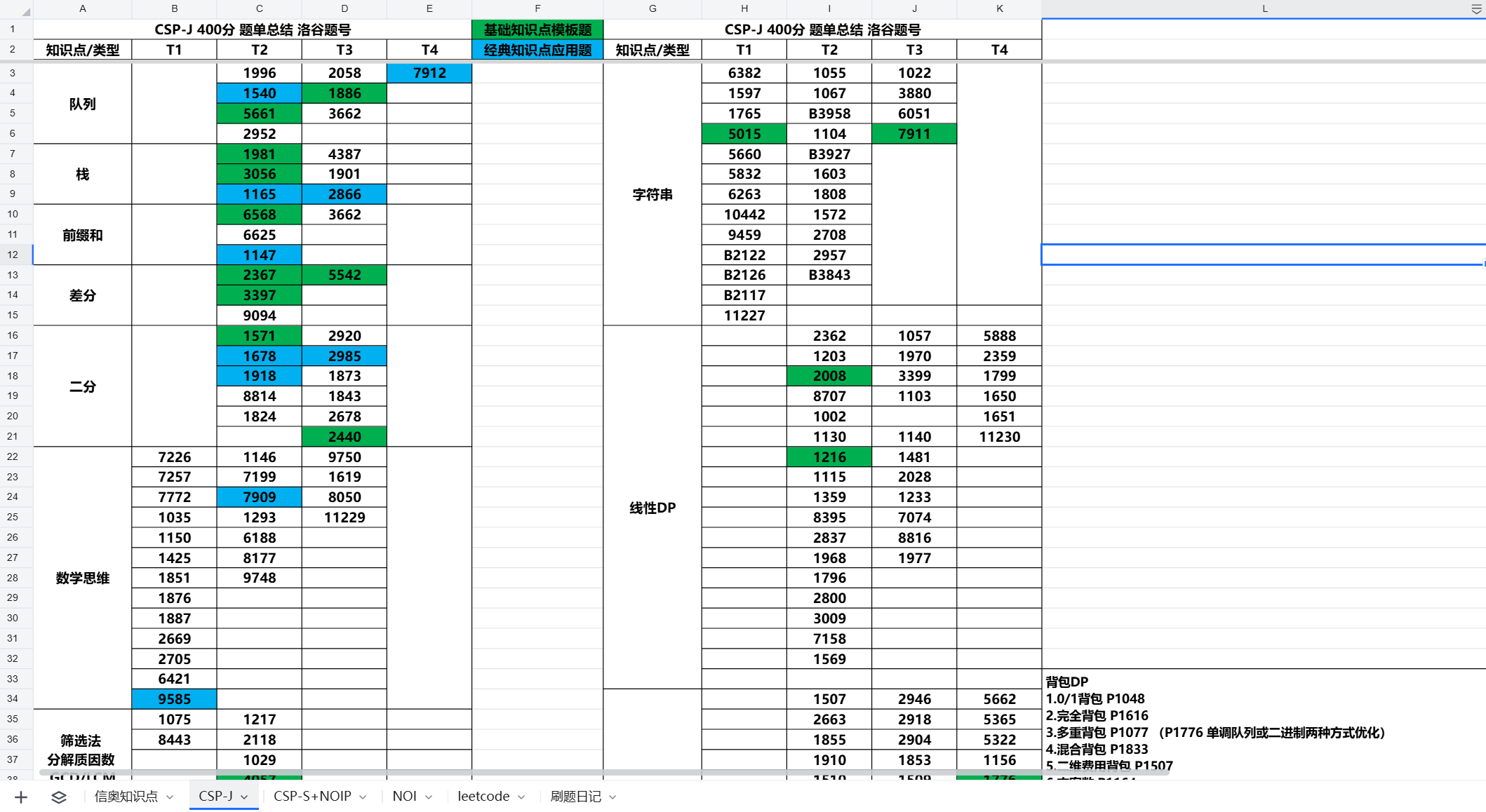
CSP-J/S

注意区分
是小学,初中 还是高中 不同阶段,有些资料没有标准学习阶段,导致让人产生误解


完整内容:https://docs.qq.com/sheet/DY1NwcGZjUXpYb01j
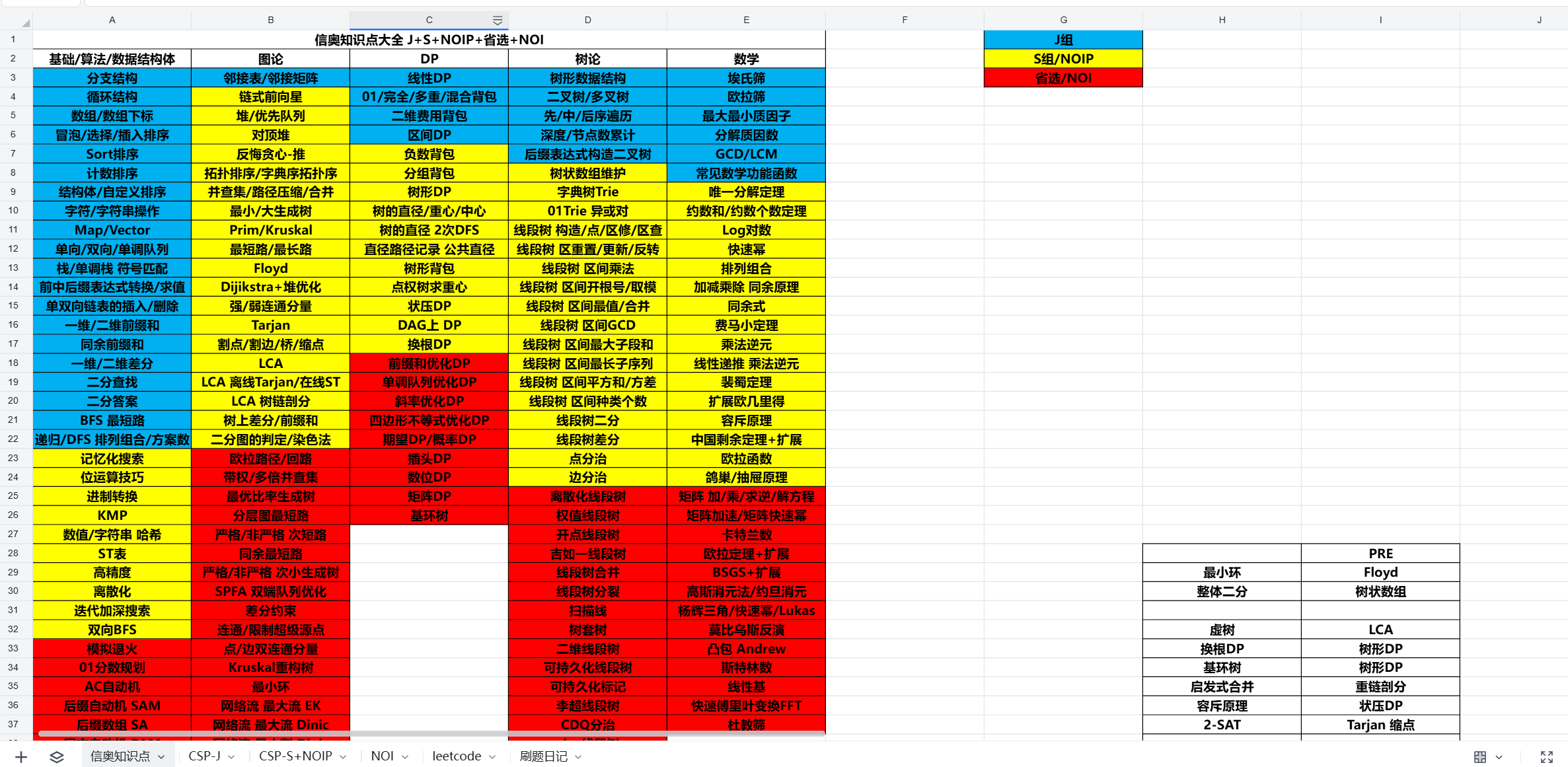
数据结构与算法 leetcode
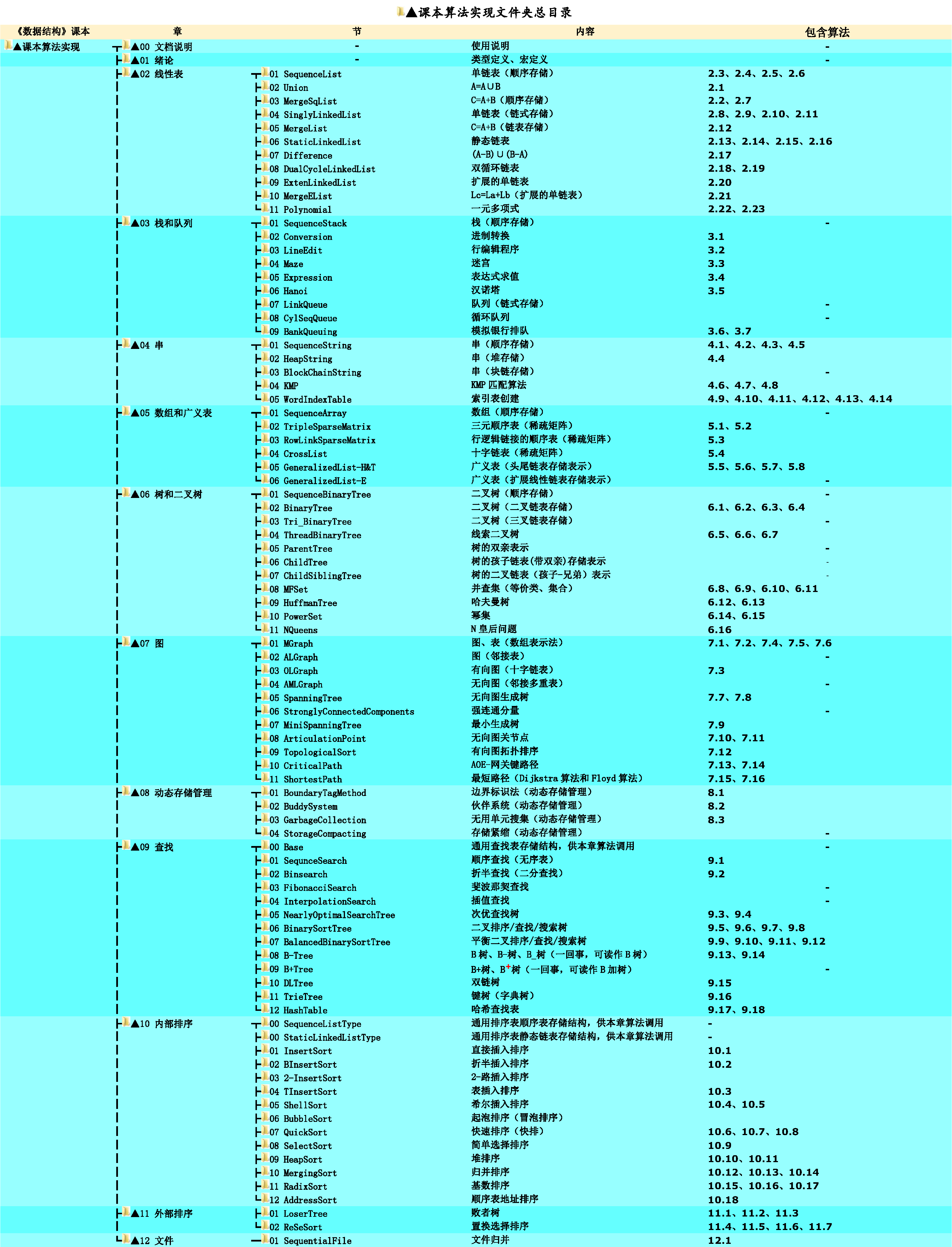
第三步:刷题日记:专心做一题
There are a total of numCourses courses you have to take,
labeled from 0 to numCourses - 1.
You are given an array prerequisites where prerequisites[i] = [ai, bi]
indicates that you must take course bi first if you want to take course ai.
For example, the pair [0, 1], indicates that to take course 0 you have to first take course 1.
Return true if you can finish all courses.
Otherwise, return false.
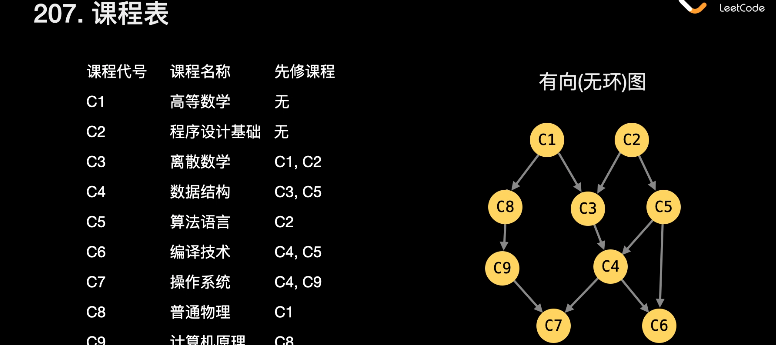
这种叫 有向无环图,把一个 有向无环图 转成 线性的排序 就叫 拓扑排序
图的存储
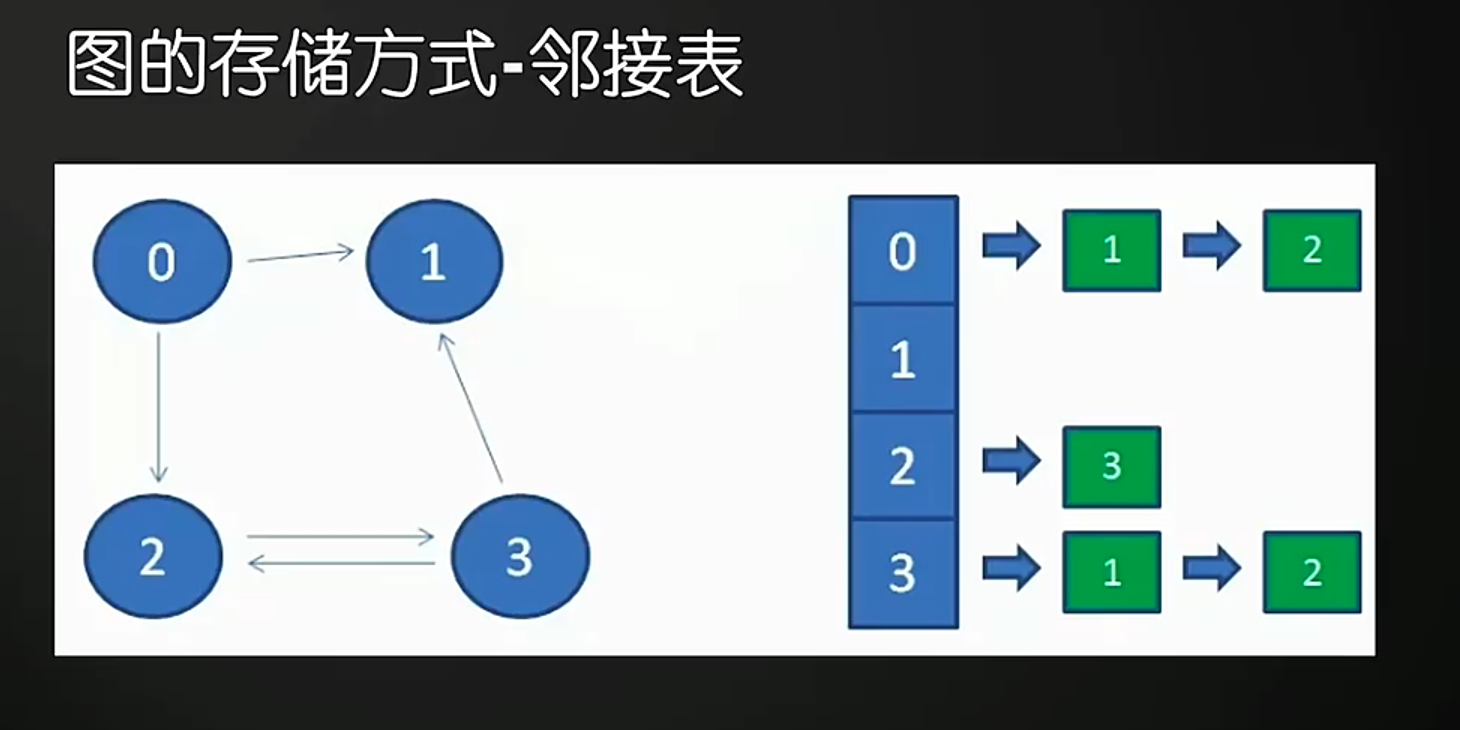
|
|
图遍历

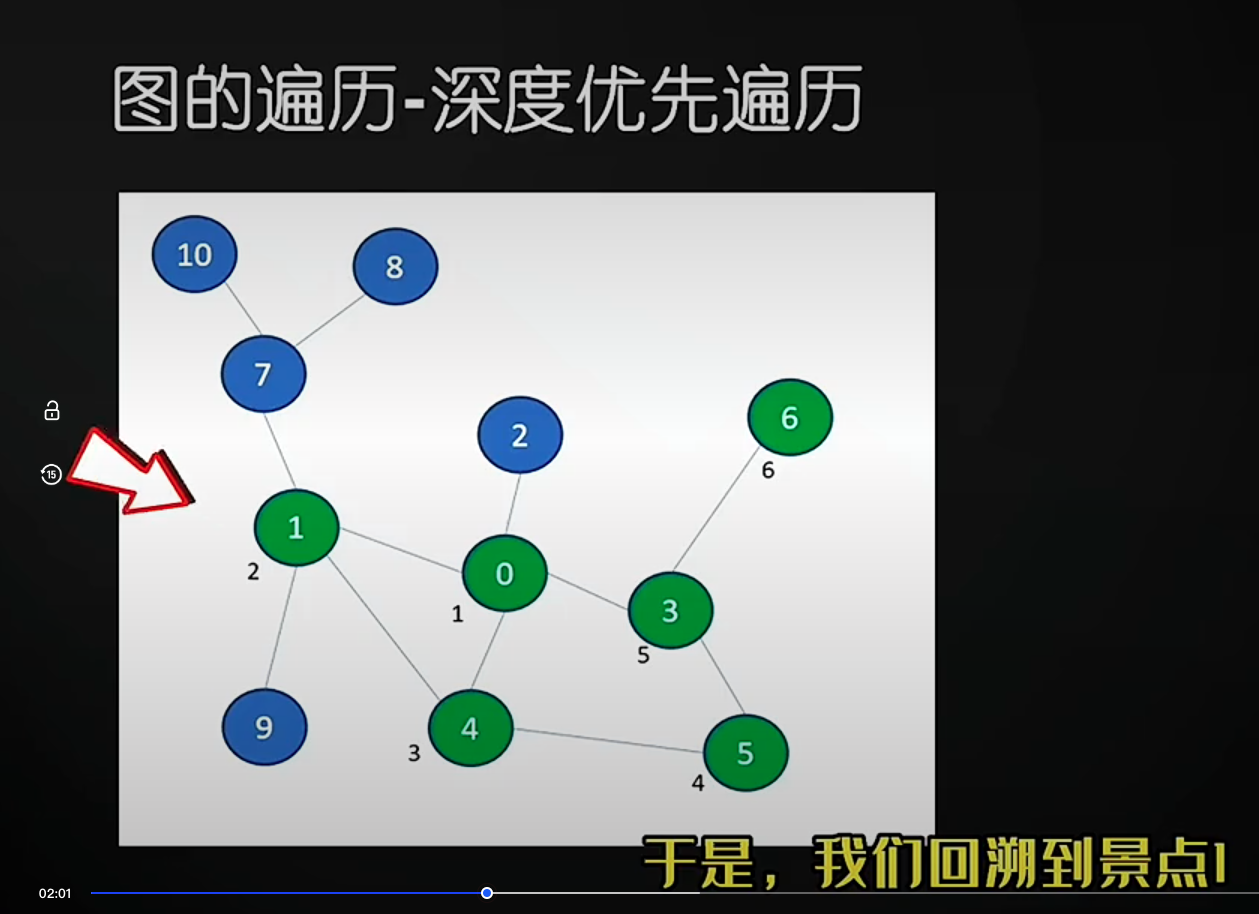
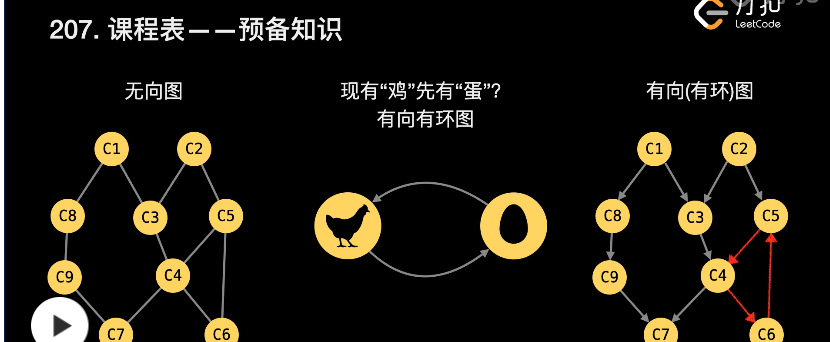
回归:# 漫画:深度优先遍历 和 广度优先遍历 https://cloud.tencent.com/developer/article/1618700?policyId=1003
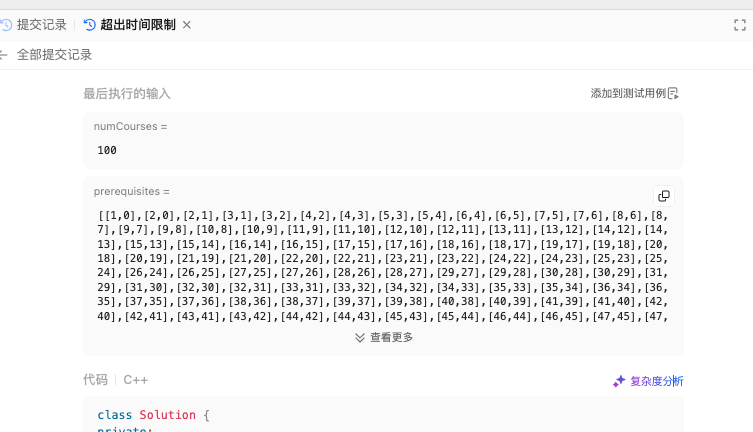
完整代码:
|
|
参考资料:
- http://ybt.ssoier.cn:8088/
- https://leetcode.cn/
- https://www.luogu.com.cn/
- https://www.nowcoder.com/
- https://www.cnblogs.com/kkman2000/p/18806934
- https://github.com/liweiwei1419/LeetCode-Solution-PPT
- 大话数据结构:https://github.com/anliux/Play-With-Data-Structure
- https://github.com/youngyangyang04/leetcode-master
- https://github.com/watchpoints/LeetCode-CSP-NOI
- https://github.com/watchpoints/noi_and_leetcode/tree/main
- 数据 结构与算法(c 语言版本)https://github.com/kangjianwei/Data-Structure https://github.com/TheAlgorithms/Python
- https://github.com/MoonShadowzzc/Data-Structure
链接我
最动人的作品,为自己而写,刚刚好打动别人 刚刚好,是最难得的美好


