哥,找你诉诉苦,目前老板直骗(boss)上打招呼的 9 个里面有 8 个外包,还有一个 OD
怎么?
刷题:
让事情变的伟大
从别动刷题到 以教促学
LeetCode CSP,NOIP 一起搞
第一步:建立大局观 刷题有什么用
第二步:构建知识地图: 针对知识点有效训练
第三步:专心刷题
第一步:建立大局观
信奥以数学为基础,本质上比拼的是算法,并指定C++作为唯一参赛编程语言
 ]()
]()
CSP、NOIP、NOI这三个比赛都是由中国计算机学会(CCF)举办的,
代表同学们在编程竞赛上的不同阶段:
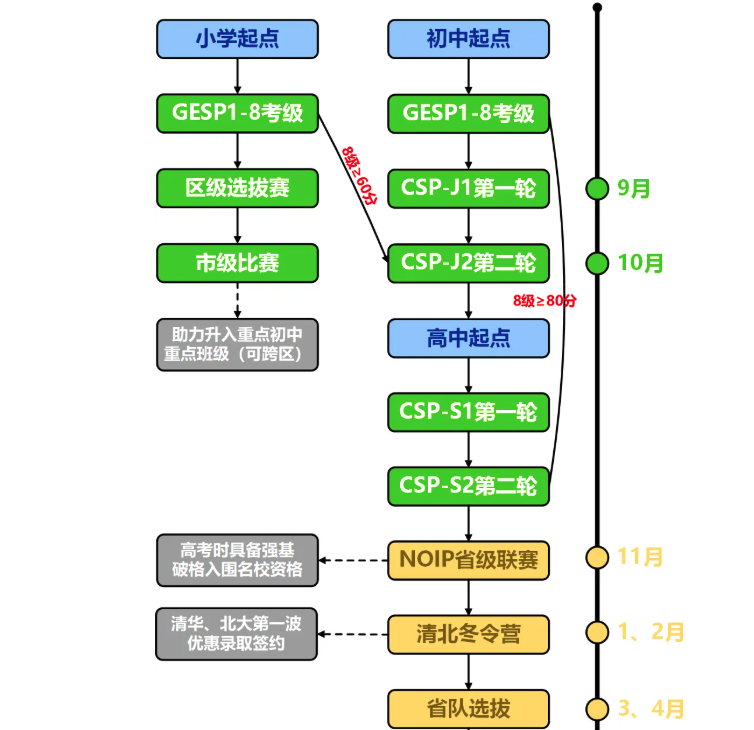
1. CSP-J(入门级,Junior) 主要针对小学和初中生
2. CSP-S(提高级,Senior)CSP-S面向高中生
3. NOIP:NOIP是参加NOI的必要条件,只能使用C++语言
4. 省内选拔(省选),NOI省选是进入NOI活动的重要环境
5. NOI(国赛)
-
CSP-S的成绩是参加NOIP(全国青少年信息学奥林匹克联赛)的主要资格来源
-
NOIP省级核心赛事,承担着筛选基础人才的任务;
-
而NOI则是国家级终极竞技场,通过层层选拔培养顶尖选手
NOI是国内最高水平的信息学竞赛
全国青少年信息学奥林匹克竞赛旨
在向那些在中学阶段学习的青少年普及计算机科学知识
给那些有才华的学生提供相互交流和学习的机会;
通过竞赛和相关的活动培养和选拔优秀计算机人才。
CSP又叫CCF非专业级软件能力认证,面向全社会,所有人都可以参加。
这项认证主要分为两个等级,CSP-J(入门级)和CSP-S(提高级)。
完整地址:https://docs.qq.com/sheet/DY1NwcGZjUXpYb01j?tab=oqi27u
使用场景与目标人群
- NOI:主要服务于中学生竞赛升学
- LeetCode:面向求职者(尤其是软件工程师)及编程爱好者,用于提升面试通过率或日常技能训练,无年龄或选拔限制。
- LeetCode 无法替代 NOI 官方题库(如《信息学奥赛一本通》或历年真题),高阶选手仍需通过针对性训练(如模拟赛、省选真题)提升实战能力
资源:
第二步:构建知识地图
当前位置:
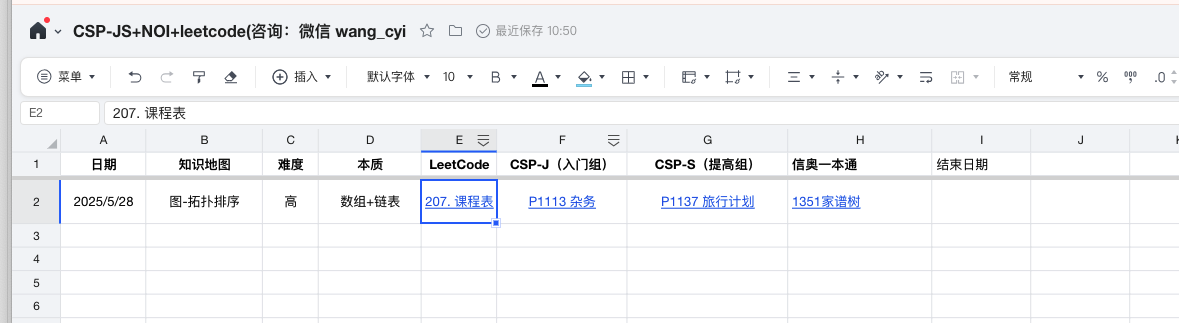
- 拓扑排序 课程表 在 leetcode ,CSP-J 和 CSP-S 对应题目
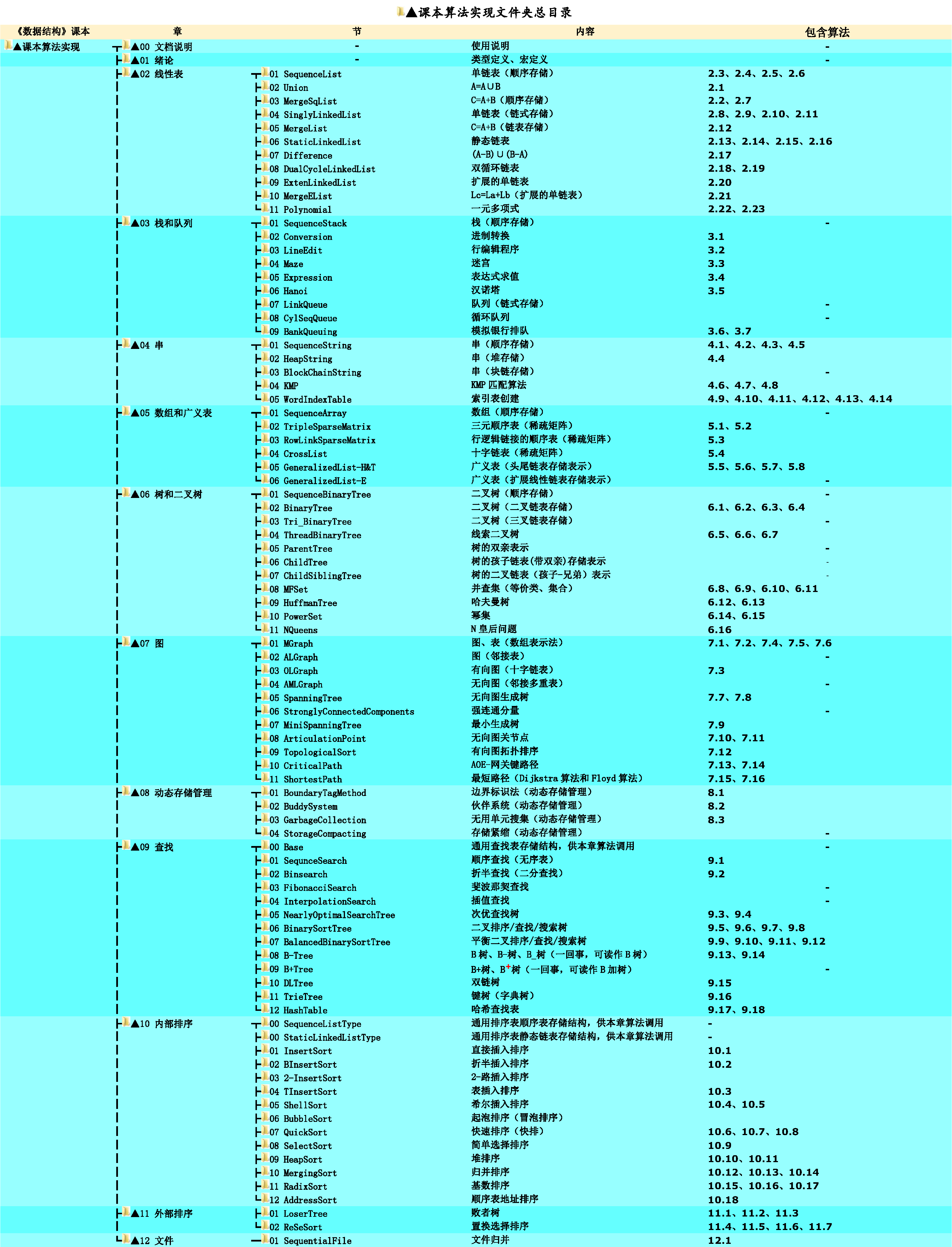
整个地图:(数据结构>(C语言版)清华大学出版社)
第三步:专心做一个题目
207. 课程表

There are a total of numCourses courses you have to take,
labeled from 0 to numCourses - 1.
You are given an array prerequisites where prerequisites[i] = [ai, bi]
indicates that you must take course bi first if you want to take course ai.
For example, the pair [0, 1], indicates that to take course 0 you have to first take course 1.
Return true if you can finish all courses.
Otherwise, return false.
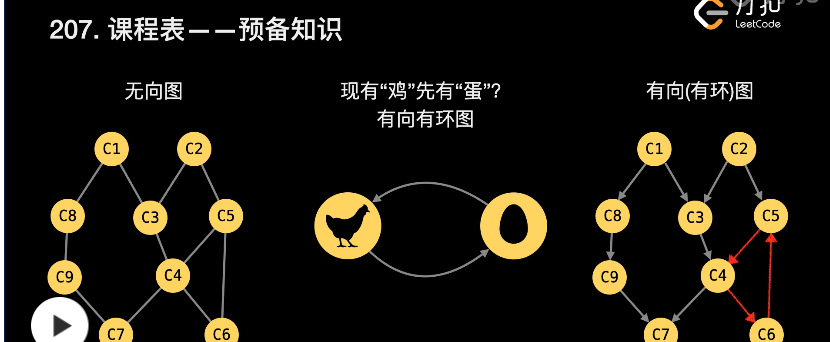
图的概念
再举个生活的例子
- 先穿内裤再穿裤子,先穿打底再穿外套,先穿衣服再戴帽子,是约定俗成的。

- 地铁:(小灰的数据结构与算法30讲)
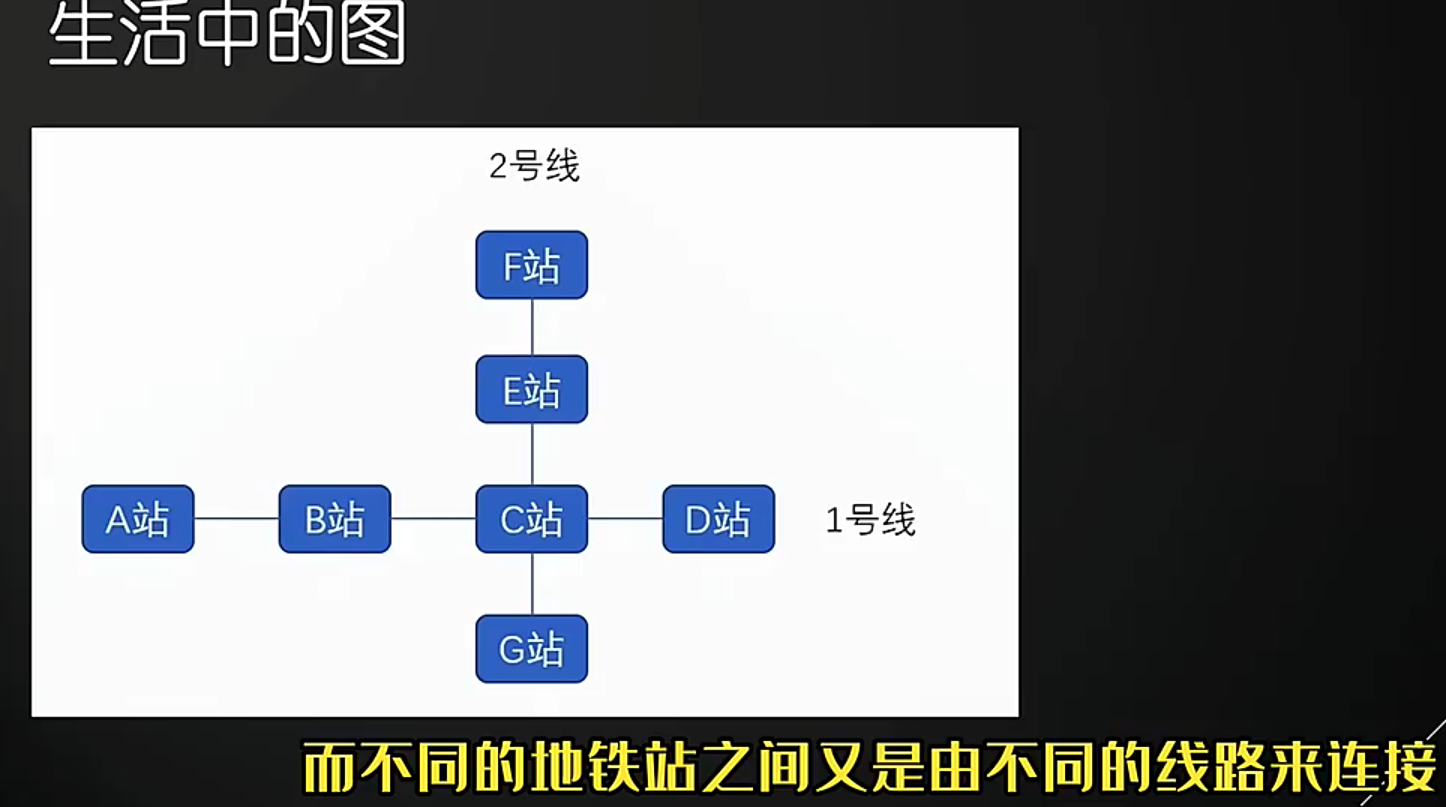
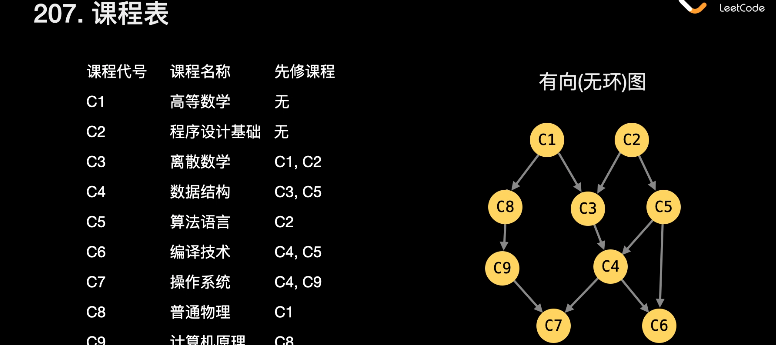
这种叫 有向无环图,把一个 有向无环图 转成 线性的排序 就叫 拓扑排序
图的存储
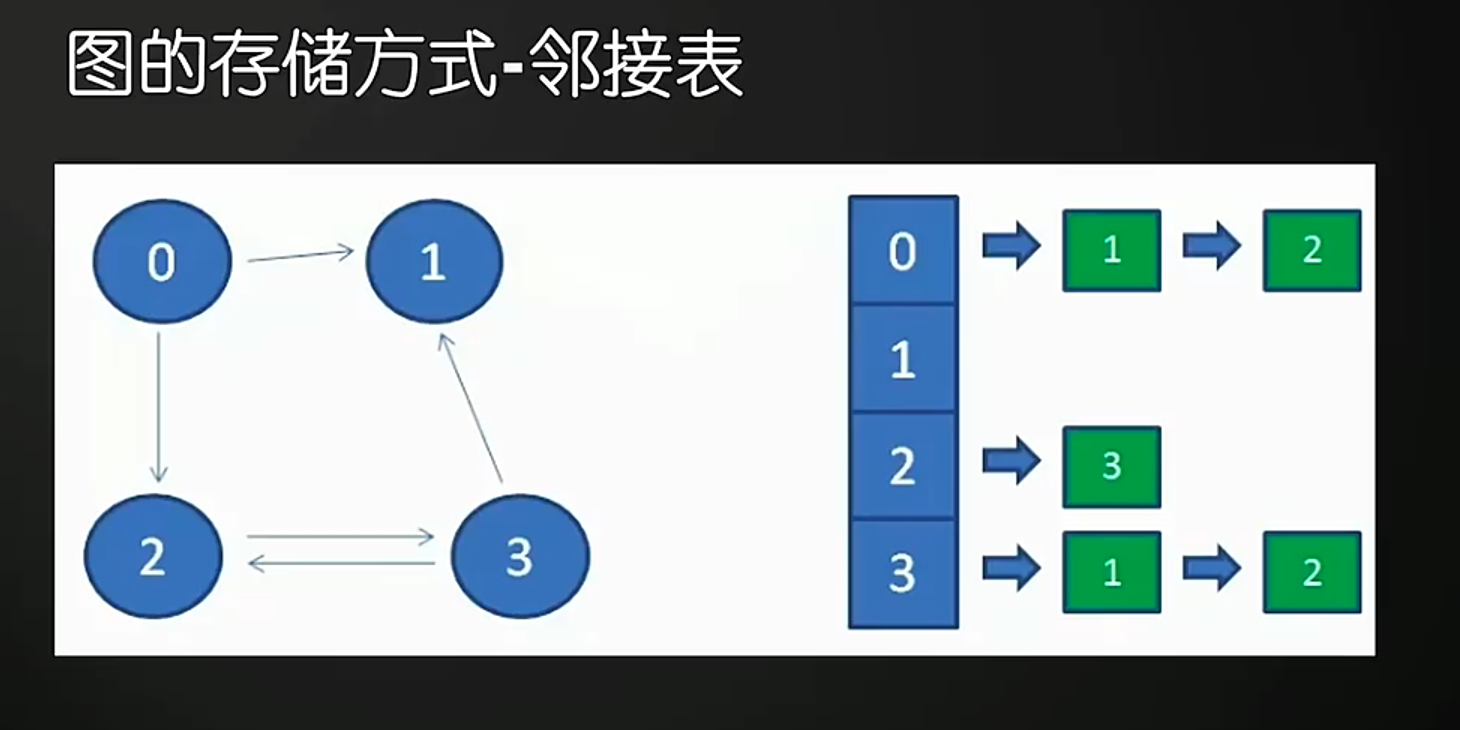
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
名字:图(Graph)
数据对象集:G( V, E )由一个非空的有限顶点集合V和一个有限边集合E组成。
操作集合:对于任意图G∈Graph,以及v∈V,e∈E 。
Graph Create():建立并返回空图;
Graph InsertVertex(Graph G , Vertex v):将v插入G;
Graph InsertEdge(Graph G , Edge e):将e挿入G;
void DES( Graph G , Vertex v ):从顶点v出发深度优先遍历图G;
void BES( Graph G , Vertex v ):从顶点v出发宽度优先遍历图G;
void ShortestPath( Graph G, Vertex v ,int Dist [ ] ):
计算图G中顶点v到任意其他顶点的最短距离;
void MST( GraphG ):
计算图G的最小生成树
|
图遍历


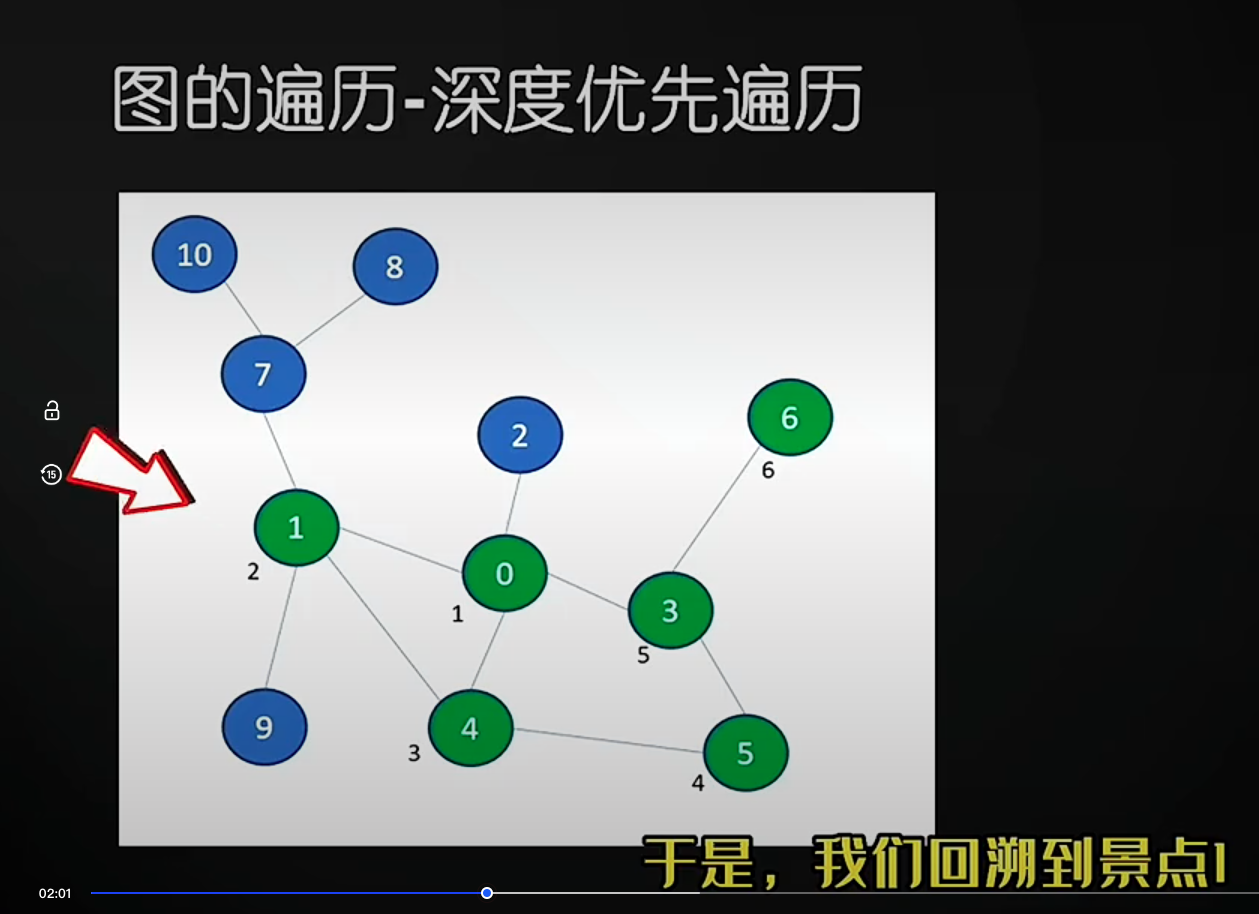
回归:# 漫画:深度优先遍历 和 广度优先遍历
https://cloud.tencent.com/developer/article/1618700?policyId=1003
-
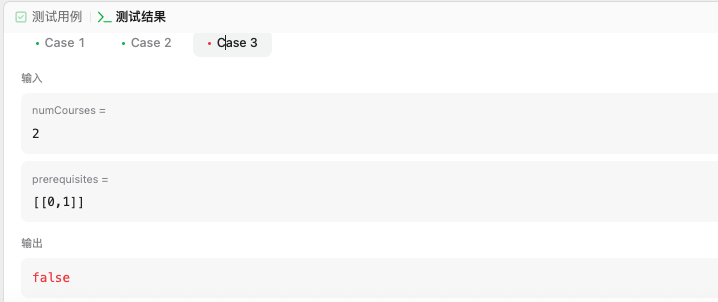
标记状态的作用:
-
0(未访问):初始状态,表示节点尚未被遍历。
-
1(访问中):临时状态,表示当前递归路径正在访问该节点。如果在后续遍历中再次遇到标记为 1 的节点,说明存在环(如 prerequisites 中存在循环依赖)。
-
2(已访问):最终状态,表示该节点及其所有子节点已安全完成遍历,无环存在。
-
每个节点遍历一遍
-
遍历一个节点,判断当前i 是否存在环节。
-
引入否存在环节判断 影响了步骤 1 的判断。
n=100 时候,数据量增加为什么执行超时
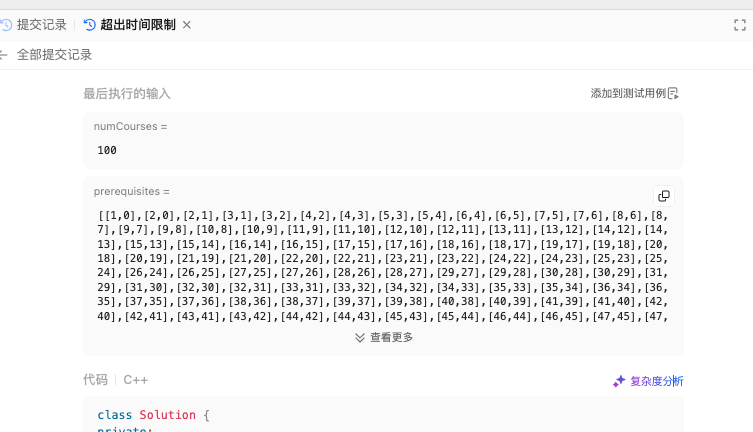
规格:递归深度
尽管图无环,但需注意:
- 递归深度:
- 若依赖链过长(如从
0 到 99 的线性链),递归深度可能达到 100 层,可能引发栈溢出(但大多数现代编程语言可处理)。
三色标记法&拓扑排序
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
|
class Solution {
private:
map<int,vector<int>> graph;
// 图的存储结构--邻居表 数组,链表,
//为了方面表示 用 map 代替数组,vecotr 代替 链表
//1 <= numCourses <= 2000
//vector<bool> visited;
// false 没有访问过 ,true访问过
//解决:维护visited集合或数组,标记已访问节点。
//如果有向无环图:每个节点只访问一次 ,不会重复遍历。
//如果有向有环图:出现部分节点重复遍历,死循环情况,这个存在环,结束循环。
// 踏平坎坷,成大道
// 斗罢艰险,又出发,又出发
//实际结果:
//1. 首先了解课表提供基本概念和算法 2 动手写这些算法 ,这个基本测试用例,正常情况下。
//3. 如果写更多测试用例 leetcode 提供了 写过程遇到bug 极端情况 更深入一步思考这个价值地方。【核心的地方 】
//
vector<int> visited; //0没有访问 1 正在访问中,包括邻居节点访问 如果回到到存在环 2 没有环,访问完成。如果下次访问时候 不需要在遍历
public:
bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
//其中 prerequisites[i] = [数据结构,C++],
//表示如果要学习课程 数据结构则 必须 先学习课程 C++,是前置条件 ,
//如果有多个前置条件呢?例如 [数据结构,c],1
//1对多,就需要图这个结构
//疑问 1:tree 也是 1 对多为什么不用 tree 呢:tree 有严格层级关系 无法表示 一个节点和剩余 n-1 个节点直接关系。
// 图是 节点之间多对对复杂网络结构
// i:每个课程 编号 ,是不是 更抽象一层。疑问 2:最后发现可能跟课程名字没关系,为什么题目给出n 个课程 ,但是没有给出课程名字,
//疑问3: 难后容易 ,还是先容易后难,课程安排 l0 l1,l2
// 节点 与节点之间关系是:i--->j 学完课程 i 之后 ,才可以学习课程 和输入好想法。数据结果中 有向图 <--- 这个方向不好表示
for(auto item:prerequisites)
{
int key = item[1]; //先完成课程,容易完成
int value = item[0];//后完成课程 ,难完成的
graph[key].push_back(value); // 图的存储结构--邻居表 数组+链表
}
//输入:numCourses = 2, prerequisites = [[1,0],[0,1]]
//输出:false
//疑问4:图的深度有限遍历,进入死胡同 前面无路可走,和 存在环 前面有路 鬼打墙 区别?
//只访问一遍原则:有向无环图(死胡同 前面无路可走) vs 有向有环图 ( 前面有路 鬼打墙)
//回答:backtrace(栈回溯)保证 前方有路就走
// 你挑着担,我牵着马
// 迎来日出,送走晚霞
// 踏平坎坷,成大道
// 斗罢艰险,又出发,又出发
// 啦啦…… ……
// 一番番春秋、冬夏。
// 一场场酸甜、苦辣。
// 敢问路在何方 路在脚下。
// 敢问路在何方 路在脚下。
//这句词源于鲁迅《故乡》中的“其实地上本没有路,走的人多了,也便成了路”
//解决:维护visited集合或数组,标记已访问节点。
//分配大小numCourses空间,初始化每个变量为 false 类似 避免频繁内存分配带来的性能损耗
visited.resize(numCourses,0);
//疑问 5:从哪里开始,二叉树 只有一个root 节点很清楚 ,图 n 个节点?
//为什么每个节点都遍历一遍?防止孤岛,不联通情况--- 这个课程和其他课程没有任何关系。
for(int index = 0; index < visited.size(); index++)
{
if(visited[index] == 0) //no visited
{
if (false == dfs(index))
{
return false ;//# 终止“鬼打墙” a-->b-->a
}
}
// }else {
// cout<<"22222";
// return false ;//# 终止“鬼打墙” 这个行代码 永远不会执行 dfs(index)访问一次 for 全部节点 访问 1次 正常2 次 访问。
// }
}
return true;
}
//从节点 index 开始 深度优先搜索 访问相关节点
bool dfs(int index)
{
if(visited[index] == 2) {
return true;
} //why?
if(visited[index] == 1) {
return false; //a--b--a
}
visited[index] = 1;
vector<int> &neight = graph[index];
//change dirction
for(int i =0;i<neight.size();i++){
if (false == dfs(neight[i])) {
return false;
}
}
visited[index] = 2;
return true;
}
};
|
链接我
最动人的作品,为自己而写,刚刚好打动别人
刚刚好,是最难得的美好

传统美德不能丢,记得点赞了,有过 gap 的小伙伴点这条看看,有多少?
 ]()
]()














